Was versteht man unter Varianz?
Die Varianz (s²) ist ein Maß für die Verschiedenheit (Variabilität) von Messwerten eines Merkmals in einer Stichprobe.
s² wird umso größer, je mehr die Messwerte vom gemeinsamen Mittelwert abweichen, also je unterschiedlicher die Messwerte sind.

s² = „mittleres Abweichungsquadrat“ (Varianz)
Wurzel aus s² = Standardabweichung (s)
n = Stichprobenumfang
i = Laufindex (i = 1, 2, …, i, … n)
xi = Messwerte
x quer = Mittelwert (Durchschnitt)
s² wird umso größer, je mehr die Messwerte vom gemeinsamen Mittelwert abweichen, also je unterschiedlicher die Messwerte sind.

s² = „mittleres Abweichungsquadrat“ (Varianz)
Wurzel aus s² = Standardabweichung (s)
n = Stichprobenumfang
i = Laufindex (i = 1, 2, …, i, … n)
xi = Messwerte
x quer = Mittelwert (Durchschnitt)
Tags: Methoden, Varianz
Source: S32
Source: S32
Was ist das Prinzip der Varianzzerlegung?
Prinzip ist interessant, weil es zeigt, wie in der Differentiellen Psychologie Kausalzusammenhänge untersucht werden können.
Zentrale Frage: Welcher Anteil der Gesamtvarianz eines
Phänomens wird durch die Varianzen der einzelnen an ihm
beteiligten Komponenten „erklärt“ - Bestimmung von
Varianzanteilen.
Dazu ein Beispiel (Hofstätter, 1977)
Weitere Komponenten (z.B. Knochenstärke) bleiben aus Vereinfachungsgründen hier unberücksichtigt.

Die Gesamtvarianz s² (kg) ist (unter Annahme, dass kh und kf unabhängig voneinander variieren) in zwei additive Komponenten (Varianzanteile) zerlegbar:
s²(kg) = s²(kg|kf) + s²(kg|kh)
100% = X% + Y%
s²(kg|kf) = Varianz des Gewichts aufgrund der Körperfülle.

Ergebnis könnte lauten:
48% von s²(kg) sind durch Körperhöhe “bedingt”,
52% durch Körperfülle (und andere Komponenten)
Analog dazu können Anlage‐ und Umweltvarianzanteile an der Gesamtvarianz eines Merkmals „M“ geschätzt werden:
s²(M) = s²(M|A) + s²(M|U) (Zwillingsforschung)
(Voraussetzungen: Kein Zusammenhang zwischen den beiden Varianzanteilen [d.h. r(A, U) = 0] und fehlerfreie Erfassung des Merkmals „M“.)
Zentrale Frage: Welcher Anteil der Gesamtvarianz eines
Phänomens wird durch die Varianzen der einzelnen an ihm
beteiligten Komponenten „erklärt“ - Bestimmung von
Varianzanteilen.
Dazu ein Beispiel (Hofstätter, 1977)
Weitere Komponenten (z.B. Knochenstärke) bleiben aus Vereinfachungsgründen hier unberücksichtigt.

Die Gesamtvarianz s² (kg) ist (unter Annahme, dass kh und kf unabhängig voneinander variieren) in zwei additive Komponenten (Varianzanteile) zerlegbar:
s²(kg) = s²(kg|kf) + s²(kg|kh)
100% = X% + Y%
s²(kg|kf) = Varianz des Gewichts aufgrund der Körperfülle.

Ergebnis könnte lauten:
48% von s²(kg) sind durch Körperhöhe “bedingt”,
52% durch Körperfülle (und andere Komponenten)
Analog dazu können Anlage‐ und Umweltvarianzanteile an der Gesamtvarianz eines Merkmals „M“ geschätzt werden:
s²(M) = s²(M|A) + s²(M|U) (Zwillingsforschung)
(Voraussetzungen: Kein Zusammenhang zwischen den beiden Varianzanteilen [d.h. r(A, U) = 0] und fehlerfreie Erfassung des Merkmals „M“.)
Tags: Methoden, Varianz, Varianzzerlegung, Zwillingsmethode
Source: S34
Source: S34
Was sollte das Modell der FA nicht auf die Daten angewandt werden?
Werden gleich viele Faktoren "extrahiert" wie Variablen in der Analyse aufgenommen wurden, dann kann zwar die "Gesamtvarianz" durch die Faktoren erklärt werden, aber eine Informationsverdichtung hat nicht stattgefunden.
Also ist zu fordern, dass die Anzahl der Faktoren (m) kleiner sein soll als die Anzahl der in die Analyse einbezogenen Variablen (k), also: m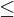 k.
k.
Bei beispielsweise k=11 Variablen beträgt die Gesamtvarianz ²ges = k = 11, weil die Variablen standardisiert sind und jeweils
²ges = k = 11, weil die Variablen standardisiert sind und jeweils  ² = 1 beitragen. Diese Überlegung ist insofern interesant, als bei der Interpretation faktorenanalytischer Ergebnisse meist gesagt wird, wie viel Prozent der Gesamtvarianz durch die extrahierten Faktoren erklärt wird.
² = 1 beitragen. Diese Überlegung ist insofern interesant, als bei der Interpretation faktorenanalytischer Ergebnisse meist gesagt wird, wie viel Prozent der Gesamtvarianz durch die extrahierten Faktoren erklärt wird.
Ist dieser Prozentsatz erklärter Gesamtvarianz gering (Faustregel: z.B. kleiner als 60%), dann sollte das Modell der FA auf diese Daten besser nicht angewandt werden.
Also ist zu fordern, dass die Anzahl der Faktoren (m) kleiner sein soll als die Anzahl der in die Analyse einbezogenen Variablen (k), also: m
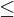 k.
k.Bei beispielsweise k=11 Variablen beträgt die Gesamtvarianz
 ²ges = k = 11, weil die Variablen standardisiert sind und jeweils
²ges = k = 11, weil die Variablen standardisiert sind und jeweils  ² = 1 beitragen. Diese Überlegung ist insofern interesant, als bei der Interpretation faktorenanalytischer Ergebnisse meist gesagt wird, wie viel Prozent der Gesamtvarianz durch die extrahierten Faktoren erklärt wird.
² = 1 beitragen. Diese Überlegung ist insofern interesant, als bei der Interpretation faktorenanalytischer Ergebnisse meist gesagt wird, wie viel Prozent der Gesamtvarianz durch die extrahierten Faktoren erklärt wird.Ist dieser Prozentsatz erklärter Gesamtvarianz gering (Faustregel: z.B. kleiner als 60%), dann sollte das Modell der FA auf diese Daten besser nicht angewandt werden.
Tags: Faktorenanalyse, Methoden, Varianz
Source: S40
Source: S40
Was wird genutzt um anzugeben, zu welchem Prozentsatz eine Eigenschaft vererbt ist? Was ist die Voraussetzung dafür?
Vorbemerkung: Es wird eine Antwort auf die Frage gesucht, zu welchem Prozentsatz Eigenschaften (traits) vererbt sind.
Dazu wird der sog. Erblichkeitsschätzer (Heritabilitätsschätzer; meist bezeichnet mit H2) bestimmt.
Die verschiedenen Formeln für H2 können je nach zugrundeliegender Modellkomplexität differieren; auch die verschiedenen Daten (Zwillingsdaten, Geschwisterdaten etc.) tragen dazu bei, dass H2 zu unterschiedlichen Ergebnissen führen kann.
Relativ einfach können Varianzanteile dadurch abgeschätzt werden, dass die Merkmalsunterschiede zwischen eineiigen Zwillingen (EZ) denjenigen von zweieiigen Zwillingen (ZZ) gegenüberstellt werden.
Voraussetzung: Umweltvarianz von EZ und ZZ ist gleich groß!
Dazu wird der sog. Erblichkeitsschätzer (Heritabilitätsschätzer; meist bezeichnet mit H2) bestimmt.
Die verschiedenen Formeln für H2 können je nach zugrundeliegender Modellkomplexität differieren; auch die verschiedenen Daten (Zwillingsdaten, Geschwisterdaten etc.) tragen dazu bei, dass H2 zu unterschiedlichen Ergebnissen führen kann.
Relativ einfach können Varianzanteile dadurch abgeschätzt werden, dass die Merkmalsunterschiede zwischen eineiigen Zwillingen (EZ) denjenigen von zweieiigen Zwillingen (ZZ) gegenüberstellt werden.
Voraussetzung: Umweltvarianz von EZ und ZZ ist gleich groß!
Tags: Erblichkeitsschätzer, Heritabilitätsschätzer, Varianz, Zwillingsmethode
Source: S150
Source: S150
Flashcard set info:
Author: coster
Main topic: Psychologie
Topic: Differentielle Psychologie
School / Univ.: Universität Wien
City: Wien
Published: 08.05.2013
Tags: WS2012/13, Georg Gittler
Card tags:
All cards (220)
16 PF (9)
Abgrenzung (1)
Adoptionsmethode (1)
Aggregation (1)
Aktivität (2)
Analysatoren (1)
Anlage/Umwelt (13)
Anwendung (4)
Army-Alpha-Test (1)
Ausdruck (1)
Beispiel (3)
Big Five (11)
Binet (5)
Carroll (2)
CAT (1)
Cattell (17)
CHC (2)
Darwin (2)
Definition (13)
EEG (2)
Einstellungstyp (1)
Entstehung (1)
Entwicklung (1)
Erblichkeit (1)
Evolution (1)
Experiment (4)
Extraversion (7)
Eysenck (14)
Faktorenanalyse (11)
Faktorenmodell (1)
Fehr (1)
Felabhängigkeit (1)
Feldabhängigkeit (2)
fMRT (1)
Forschung (22)
Fragebogen (1)
Funktionstyp (1)
Galton (3)
Gardner (3)
Geschichte (11)
Gray (1)
HAWIE (1)
Hochbegabung (4)
Hofstätter (2)
Horn (3)
Intelligenz (41)
Intelligenzmodelle (17)
Intervention (1)
Jung (6)
Kagan (1)
Kelly (4)
Korrelation (5)
Kretschmer (1)
Kritik (12)
Mendel (1)
mental Speed (3)
mental speed (1)
Merkmal (1)
Methoden (22)
Neurotizismus (3)
Normalverteilung (1)
Norman (1)
Objektivität (1)
Persönlichkeit (36)
Persönlickeit (1)
PET (1)
Prozessmodell (1)
Psychographie (2)
Psychologie (2)
Psychometrie (1)
Psychotizismus (2)
Quasi-Experiment (1)
R/S Konstrukt (4)
Rasch-Modell (17)
Reflexivität (1)
Regression (2)
Repression (2)
Rogers (7)
Sensitization (2)
Sheldon (1)
Simon-Binet-Test (1)
Skala (1)
Spearman (4)
Stabilität (1)
Stern (10)
Sternberg (6)
Stimmung (1)
Strelau (3)
Streuung (1)
Struktur (1)
Superfaktoren (1)
Terman (2)
Test (10)
Testung (1)
Theorie (6)
Thurstone (2)
TMI (3)
Trait-Modell (7)
Typenlehre (1)
Unterschiede (1)
Variable (1)
Varianz (4)
Varianzzerlegung (1)
Vernon (2)
Wahrnehmung (1)
Wechsler (2)
Witkin (1)
working memory (2)
Zuckerman (3)
Zwillingsmethode (5)



