Erkläre anhand eines Gedankenexperiments die Idee der Faktorenanalyse?
Datenerhebung an n Vpn mit k = 5 Messinstrumenten (Variable):
Beobachtung in der Interkorrelationsmatrix (k x k): 3 Variable (Thermometer) sind hoch korreliert (|r| → 1.0), ebenso die beiden anderen (Puls). Zwischen Variablen, entnommen aus jeweils einer Variablengruppe, liegen jedoch nur niedrige Korrelationen vor (|r| → 0.0).
FA wird durchgeführt; Fragestellung: Wie viele unabhängige Faktoren (Dimensionen, Eigenschaften, Konstrukte) sind (minimal) notwendig, um die Zusammenhänge in den fünf Variablen zu „erklären“?
Ergebnis (Gedankenexperiment): Die Daten können durch 2 Faktoren „erklärt“ werden.
Auf 1. Faktor „laden“ 3 Variable (Thermometer) hoch [d.h. sind mit dem Faktor hoch korreliert], auf 2. Faktor laden die Pulsmessungen hoch.
Allgemein: m Faktoren, wobei m < k - FA dient der Informationsverdichtung!
Interpretation: Die fünf Messinstrumente messen nur 2 unabhängige Dimensionen (Eigenschaften, Faktoren). Drei etablieren den 1. Faktor, zwei den 2. Faktor. Weil wir wissen, was die Messinstrumente messen ist hier die inhaltliche Interpretation leicht - Körpertemperatur (Fakt.1) und
Herzschläge/min (Fakt.2).
Folgerung: Zukünftig wird es nicht mehr notwendig sein, alle fünf Messinstrumente zu verwenden; eines für Faktor 1 und ein zweites für Faktor 2 werden genügen. (Stichworte: Datenverdichtung und Datenreduktion als Ziel der FA)
Beachte: Hätten wir ein Hygrometer hinzugenommen, wäre ein dritter Faktor (Luftfeuchtigkeit) resultiert. - Es können also nur jene Eigenschaften faktorenanalytisch gewonnen (=extrahiert) werden, die in den in den Analysen aufgenommenen Variablen enthalten sind.
- 3 Thermometer (mit verschiedenen Skalen: Kelvin, Fahrenheit, Celsius)
- 2 Pulsmessungen (durch Arzt / mittels Pulsmessgerät)
Beobachtung in der Interkorrelationsmatrix (k x k): 3 Variable (Thermometer) sind hoch korreliert (|r| → 1.0), ebenso die beiden anderen (Puls). Zwischen Variablen, entnommen aus jeweils einer Variablengruppe, liegen jedoch nur niedrige Korrelationen vor (|r| → 0.0).
FA wird durchgeführt; Fragestellung: Wie viele unabhängige Faktoren (Dimensionen, Eigenschaften, Konstrukte) sind (minimal) notwendig, um die Zusammenhänge in den fünf Variablen zu „erklären“?
Ergebnis (Gedankenexperiment): Die Daten können durch 2 Faktoren „erklärt“ werden.
Auf 1. Faktor „laden“ 3 Variable (Thermometer) hoch [d.h. sind mit dem Faktor hoch korreliert], auf 2. Faktor laden die Pulsmessungen hoch.
Allgemein: m Faktoren, wobei m < k - FA dient der Informationsverdichtung!
Interpretation: Die fünf Messinstrumente messen nur 2 unabhängige Dimensionen (Eigenschaften, Faktoren). Drei etablieren den 1. Faktor, zwei den 2. Faktor. Weil wir wissen, was die Messinstrumente messen ist hier die inhaltliche Interpretation leicht - Körpertemperatur (Fakt.1) und
Herzschläge/min (Fakt.2).
Folgerung: Zukünftig wird es nicht mehr notwendig sein, alle fünf Messinstrumente zu verwenden; eines für Faktor 1 und ein zweites für Faktor 2 werden genügen. (Stichworte: Datenverdichtung und Datenreduktion als Ziel der FA)
Beachte: Hätten wir ein Hygrometer hinzugenommen, wäre ein dritter Faktor (Luftfeuchtigkeit) resultiert. - Es können also nur jene Eigenschaften faktorenanalytisch gewonnen (=extrahiert) werden, die in den in den Analysen aufgenommenen Variablen enthalten sind.
Tags: Faktorenanalyse, Methoden
Quelle: S38
Quelle: S38
Was ist die Ziel bzw. die Idee der Faktorenanalyse?
Die Faktorenanalyse (FA) ist ein Verfahren zur Informationsverdichtung (wissenschaftliche Ökonomisierung) mit dem Ziel, die, einem Variablensatz (= manifeste Variable) zugrunde liegende Dimensionen (=latente Variable bzw. Konstrukte, Faktoren, Eigenschaften) rechnerisch zu ermitteln.
Ausgangspunkt sind die standardisierten Variablen und deren Interkorrelationen (Korrelationen zwischen allen Paaren von Variablen). FA versucht die (linearen) Zusammenhänge (Interkorrelationen), die zwischen Variablen bestehen, einfacher zu erklären, indem diese Zusammenhänge auf wenige gemeinsame Faktoren zurückgeführt werden.

Ausgangspunkt sind die standardisierten Variablen und deren Interkorrelationen (Korrelationen zwischen allen Paaren von Variablen). FA versucht die (linearen) Zusammenhänge (Interkorrelationen), die zwischen Variablen bestehen, einfacher zu erklären, indem diese Zusammenhänge auf wenige gemeinsame Faktoren zurückgeführt werden.

Tags: Faktorenanalyse, Methoden
Quelle: S38
Quelle: S38
Wie ist die Vorgehensweise bei der Faktorenanalyse?

Standardisierung der Ausgangsdaten
Variable, die in FA eingehen, haben unterschiedlich große Varianzen s² bzw.
 ² (Populationsschätzer).
² (Populationsschätzer).Da für die k Variable Varianzanteile bestimmt werden sollen, die sich durch m gemeinsame Faktoren erklären lassen, müssen zunächst die s2 „vereinheitlicht“ werden.
Das geschieht ohne Informationsverlust (Korrelationen sind invariant gegenüber linearer Messwerttransformation) durch Standardisierung jeder Variable:

Korrelationsmatrix
Die Korrelationen zwischen je zwei standardisierten Variablen seien durch „Überlappungsbereiche“ dargestellt:

Für jede Variable ergibt sich ein „Geflecht“ von Überlappungen und jeweils einem variablespezifischen, eigenständigen Bereich („uniqueness“).
FA soll dieses „Geflecht“ einfacher strukturieren, also „Gemeinsames“ von „Speziellem“ trennen.
Die Faktoren werden üblicherweise so bestimmt, dass sie miteinander nicht korreliert sind (= „orthogonale“ Faktoren).
Der 1. Faktor soll größtmögliche Überlappungen aller Variablen „umfassen“, dann 2. Faktor … usw.
Beispiel für zwei Variable:

Diesen Varianzanteilen entsprechen sog. Ladungszahlen
aij² = Varianzanteil des j‐ten Faktors an Variable Xi ; oder Ausmaß, in dem die Variable Xi mit dem latenten Faktor Fj zusammenhängt). [aij² - zu interpretieren wie Korrelationen mit Werten zwischen ‐1 und +1]
Ziel ist die Berechnung der Faktorenladungsmatrix (k Var., m Fakt., mit m < k):
Aus den der Größe nach geordneten Ladungszahlen kann auf die inhaltliche Interpretation des jeweiligen Faktors rückgeschlossen werden.
Überlegung: Werden genau so viele Faktoren „extrahiert“ wie Variable einbezogen wurden, dann kann zwar 100% der „Gesamtvarianz“ (= k) durch die Faktoren erklärt werden, aber eine Informationsverdichtung hat nicht stattgefunden (daher Forderung: m < k).
Methode = Extremwertaufgabe mit der Idee, dass möglichst
wenige Faktoren möglichst viel der Gesamtvarianz erklären.
Lösung führt zu Eigenwertproblem, das in numerischer
Statistik bekannt ist (iteratives Vorgehen zur Schätzung
der Ladungen).
Tags: Faktorenanalyse, Methoden
Quelle: S40
Quelle: S40
Was sind die Prinzipien der Faktorenanalyse?
Die m gemeinsamen Faktoren werden so bestimmt, dass …
- … der durch sie erklärte Varianzanteil maximal ist;
- … sie statistisch unkorreliert sind (orthogonal);
- … sie Einfachstruktur (simple structure) aufweisen, d.h. nach Rotation des Achstensystems, soll jeder Faktor in einigen Variablen hohe Ladungen und sonst vorwiegend Null‐Ladungen aufweisen - das dient der besseren Interpretierbarkeit: die Variablen mit hohen Ladungen (= Markervariablen) „beschreiben“ (determinieren) inhaltlich den Faktor
Tags: Faktorenanalyse, Methoden
Quelle: S40
Quelle: S40
Was sollte das Modell der FA nicht auf die Daten angewandt werden?
Werden gleich viele Faktoren "extrahiert" wie Variablen in der Analyse aufgenommen wurden, dann kann zwar die "Gesamtvarianz" durch die Faktoren erklärt werden, aber eine Informationsverdichtung hat nicht stattgefunden.
Also ist zu fordern, dass die Anzahl der Faktoren (m) kleiner sein soll als die Anzahl der in die Analyse einbezogenen Variablen (k), also: m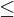 k.
k.
Bei beispielsweise k=11 Variablen beträgt die Gesamtvarianz ²ges = k = 11, weil die Variablen standardisiert sind und jeweils
²ges = k = 11, weil die Variablen standardisiert sind und jeweils  ² = 1 beitragen. Diese Überlegung ist insofern interesant, als bei der Interpretation faktorenanalytischer Ergebnisse meist gesagt wird, wie viel Prozent der Gesamtvarianz durch die extrahierten Faktoren erklärt wird.
² = 1 beitragen. Diese Überlegung ist insofern interesant, als bei der Interpretation faktorenanalytischer Ergebnisse meist gesagt wird, wie viel Prozent der Gesamtvarianz durch die extrahierten Faktoren erklärt wird.
Ist dieser Prozentsatz erklärter Gesamtvarianz gering (Faustregel: z.B. kleiner als 60%), dann sollte das Modell der FA auf diese Daten besser nicht angewandt werden.
Also ist zu fordern, dass die Anzahl der Faktoren (m) kleiner sein soll als die Anzahl der in die Analyse einbezogenen Variablen (k), also: m
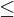 k.
k.Bei beispielsweise k=11 Variablen beträgt die Gesamtvarianz
 ²ges = k = 11, weil die Variablen standardisiert sind und jeweils
²ges = k = 11, weil die Variablen standardisiert sind und jeweils  ² = 1 beitragen. Diese Überlegung ist insofern interesant, als bei der Interpretation faktorenanalytischer Ergebnisse meist gesagt wird, wie viel Prozent der Gesamtvarianz durch die extrahierten Faktoren erklärt wird.
² = 1 beitragen. Diese Überlegung ist insofern interesant, als bei der Interpretation faktorenanalytischer Ergebnisse meist gesagt wird, wie viel Prozent der Gesamtvarianz durch die extrahierten Faktoren erklärt wird.Ist dieser Prozentsatz erklärter Gesamtvarianz gering (Faustregel: z.B. kleiner als 60%), dann sollte das Modell der FA auf diese Daten besser nicht angewandt werden.
Tags: Faktorenanalyse, Methoden, Varianz
Quelle: S40
Quelle: S40
Was ist das multiple FA-Modell?
von Garnett, 1919; weiterentwickelt von Thurstone, 1931, 1935

F1, F2, ... Fm - "common factors" (latente Eigenschaften)
Si - spezifische Faktoren des Tests Xi
 i - Fehlerterm des Tests Xi
i - Fehlerterm des Tests Xi
Die Ladungszahlen aij (bzw. deren Quadrat) können auf drei verschiedene Arten interpretiert werden:

F1, F2, ... Fm - "common factors" (latente Eigenschaften)
Si - spezifische Faktoren des Tests Xi
 i - Fehlerterm des Tests Xi
i - Fehlerterm des Tests XiDie Ladungszahlen aij (bzw. deren Quadrat) können auf drei verschiedene Arten interpretiert werden:
- aij = Gewicht des Faktors Fj für die Variabe Xi
- aij = Korrelation des Faktors Fj mit der Variable Xi
- aij² = Varianzanteil der i-ten Variable, der durch den Faktor erklärt wird
Tags: Faktorenanalyse, Methoden
Quelle: S40
Quelle: S40
Welche zwei Typen der Faktorenanalyse können unterschieden werden?
Exploratorisch (hypothesenerkundend)
Exploratorische FA soll latente Faktorenstruktur einer Menge korrelierender Variablen „erkunden“. Spezielles Vorwissen (z.B. zur Anzahl von Faktoren) besteht nicht. Das Vorgehen ist also deskriptiv.
Konfirmatorisch (hypothesenprüfend)
Konfirmatorische FA hat zum Ziel, eine apriori bestehende Faktorenstruktur (z.B. aus Literatur bekannt) auf Verträglichkeit mit neuen empirischen Daten zu prüfen.
Das Vorgehen ist Hypothesen geleitet, inferenzstatistische Schlussfolgerungen sind möglich.
Anmerkung: Auch die konfirmatorische FA sagt nichts darüber aus, ob eine gefundene Faktorenstruktur auch die einzige gültige Struktur darstellt.
Exploratorische FA soll latente Faktorenstruktur einer Menge korrelierender Variablen „erkunden“. Spezielles Vorwissen (z.B. zur Anzahl von Faktoren) besteht nicht. Das Vorgehen ist also deskriptiv.
Konfirmatorisch (hypothesenprüfend)
Konfirmatorische FA hat zum Ziel, eine apriori bestehende Faktorenstruktur (z.B. aus Literatur bekannt) auf Verträglichkeit mit neuen empirischen Daten zu prüfen.
Das Vorgehen ist Hypothesen geleitet, inferenzstatistische Schlussfolgerungen sind möglich.
Anmerkung: Auch die konfirmatorische FA sagt nichts darüber aus, ob eine gefundene Faktorenstruktur auch die einzige gültige Struktur darstellt.
Tags: Faktorenanalyse, Methoden
Quelle: S41
Quelle: S41
Welche Arten von Faktorenmodellen gibt es?
- Generalfaktorenmodell
- Modell gemeinsamer bzw. multipler Faktoren
- Gruppenfaktorenmodell
- Faktoren zweiter bzw. höherer Ordnung

Tags: Faktorenanalyse, Faktorenmodell
Quelle: S41
Quelle: S41
Was sind grundsätzliche Probleme bzw. Kritik an der Faktorenanalyse?
Stichprobenabhängigkeit der Ergebnisse (weil korrelationsbasiert):
Variableneinbezug
Kein verbindliches Abbruchkriterium zur Faktorenextraktion
Faktorenbenennung und –interpretation: Abhängig vom Versuchsleiter.
Rotationstechniken: Schiefwinkelig (nicht sehr gebräuchlich) vs. orthogonal.
Additiv kompensatorisches Modell: Diese Modellvorstellung kann – muss aber nicht – für die Daten passend sein. Die Güte der gefundenen Lösung ergibt sich aus der durch die Faktoren aufgeklärten Varianz (Richtwert: mind. 60%).
- Vielfache Interpretationsuneindeutigkeit faktorenanalytischer Lösungen!!
- homogene Stichproben führen zu größerer Faktorenzahl mit niedrigeren Ladungen
- heterogene Stichproben führen zu geringerer Faktorenzahl mit höheren Ladungen
Variableneinbezug
- Welche? (z.B. wenn Kreativität nicht in FA aufgenommen wird, kann sie auch nicht als Intelligenzfaktor resultieren)
- Auf welchem Abstraktionsniveau: Test Score‐Niveau oder Einzelitem‐Niveau (in letzterem Fall müssen Items mit mehr als 2 Antwortmöglichkeiten gegeben sein).
Kein verbindliches Abbruchkriterium zur Faktorenextraktion
- Wie viele Faktoren erklären die Daten am besten?
- Es gibt zwar Kriterien zur Begrenzung der Faktorenzahl, diese können jedoch einander widersprechen.
Faktorenbenennung und –interpretation: Abhängig vom Versuchsleiter.
Rotationstechniken: Schiefwinkelig (nicht sehr gebräuchlich) vs. orthogonal.
Additiv kompensatorisches Modell: Diese Modellvorstellung kann – muss aber nicht – für die Daten passend sein. Die Güte der gefundenen Lösung ergibt sich aus der durch die Faktoren aufgeklärten Varianz (Richtwert: mind. 60%).
- Vielfache Interpretationsuneindeutigkeit faktorenanalytischer Lösungen!!
Tags: Faktorenanalyse, Kritik
Quelle: VO05
Quelle: VO05
Welchen Ansatz verfolgen die faktorenanalytischen Persönlichkeitstheorien?
Aufgrund der Nachteile von Typologien ergibt sich die Frage, wie viele Dimensionen ausreichen würden, um Individuen psychologisch zutreffend beschreiben zu können - genauer gesagt ergeben sich 2 wichtige Fragestellungen für die Persönlichkeitspsychologie:
Zahl der Dimensionen
In einem k‐fach abgestuften System mit d Dimensionen können kd Personen individuell (d.h. als eigene Kategorie) beschrieben werden.
Die Zahl der benötigten Dimensionen bei gegebener Zahl von Stufen und Individuen lässt sich errechnen:
d = log P / log k.

Zahl der Abstufungen je Dimension
Nach Miller (1956; „magical number 7“) kann angenommen werden, dass k = 7 ± 2 Stufen pro Dimension sicher diskriminiert werden können
(Anzahl der Antwortkategorien in Fragebögen sollte ca. 5‐9 sein).
Da in der Population die Personen bzgl. der k Abstufungen je Dimension nicht gleichverteilt sind, sondern erfahrungsgemäß einer NV folgen, muss entweder d oder k ein wenig erhöht werden, um den entstehenden „Diskriminationsverlust“ auszugleichen.
- Wollte man z.B. ca. 6 Milliarden Menschen individuell beschreiben, so ergibt sich bei k = 5, k = 7 bzw. k = 9 Stufen eine Dimensionszahl von d = 14, d = 12 bzw. d = 10.
- Ein entsprechend komplexes Klassifikationssystem (mit d = 16) wurde z.B. von R. B. Cattell entwickelt (16 PF Fragebogen).
- Wie viele Dimensionen werden zu einer theoretisch befriedigenden Unterscheidung von Individuen (Persönlichkeiten) benötigt)
- Wie viele Stufen pro Dimension sollten vorhanden sein, damit verlässlich diskriminiert (d.h. zwischen Menschen unterschieden) werden kann?
Zahl der Dimensionen
In einem k‐fach abgestuften System mit d Dimensionen können kd Personen individuell (d.h. als eigene Kategorie) beschrieben werden.
Die Zahl der benötigten Dimensionen bei gegebener Zahl von Stufen und Individuen lässt sich errechnen:
d = log P / log k.

Zahl der Abstufungen je Dimension
Nach Miller (1956; „magical number 7“) kann angenommen werden, dass k = 7 ± 2 Stufen pro Dimension sicher diskriminiert werden können
(Anzahl der Antwortkategorien in Fragebögen sollte ca. 5‐9 sein).
Da in der Population die Personen bzgl. der k Abstufungen je Dimension nicht gleichverteilt sind, sondern erfahrungsgemäß einer NV folgen, muss entweder d oder k ein wenig erhöht werden, um den entstehenden „Diskriminationsverlust“ auszugleichen.
- Wollte man z.B. ca. 6 Milliarden Menschen individuell beschreiben, so ergibt sich bei k = 5, k = 7 bzw. k = 9 Stufen eine Dimensionszahl von d = 14, d = 12 bzw. d = 10.
- Ein entsprechend komplexes Klassifikationssystem (mit d = 16) wurde z.B. von R. B. Cattell entwickelt (16 PF Fragebogen).
Tags: Faktorenanalyse, Persönlichkeit
Quelle: S95
Quelle: S95
Was sind Stärken und Schwächen der traitorientierten, faktorenanalytisch begründeten Ansätze?
Stärken - es handelt sich tatsächlich um fundierte Theorien
Schwächen
- Expliziertheit der Begriffe liegt vor (Prüfbarkeit ist gegeben)
- Sparsamkeit ist je nach Abstraktionsniveau mehr oder weniger gegeben
- Vollständigkeit wurde zumindest angestrebt
- Widerspruchsfreiheit innerhalb der einzelnen Theorien ist zum großen Teil gegeben, theorieübergreifend jedoch nur bedingt (u.a. wegen verschiedener Operationalisierung)
- Anwendbarkeit und prognostischen Wert kann aufgrund des jahrzehntelangen, vielfachen wie vielfältigen Einsatz der Fragebogen, die auf diesen Theorien basieren, angenommen werden; dass dies nicht zu unkritisch gesehen werden darf, zeigen ständige Weiterentwicklung (Fragebogenrevision und -neukonstruktionen).
- Forschungsanleitende Produktivität ist immens hoch
- Berücksichtigung verschiedener Datenquellen (L, Q, T und physiologische Maße)
- Die Unterschiedlichkeit und Widersprüchlichkeit der Theorien kann großteils auf das unterschiedliche Abstraktionsniveaus der Betrachtungsweise von Traits zurückgeführt werden. Andererseits sind sind aber auch viele Gemeinsamkeiten gegeben - neuere Forschung bemüht sich um Integration.
Schwächen
- Konzept des "Persönlichkeitswesenzugs" (Trait-Konzept) geht von transsituativer Konsistenz der Verhaltensweisen aus; dadurch wird die systematische Untersuchung der Beziehung von spezifischen Situationen zu latenten Traits bzw. manifestem Verhalten tlw. vernachlässigt (- Situationismus; Interaktionismus)
- Die Faktorenanalyse mit ihren grundlegenden Problemen ist nur bedingt geeignet, ein allgemeingültiges Beschreibungssystem für Persönlichkeit zu begründen. (Probleme: Stichprobenabhängigkeit, Roationstechniken, Faktorenextraktion, Interpretation, Variablenbezug) - Interpretationsuneindeutigkeit faktorenanalytischer Lsungen
- Das Vorliegen einer Fülle von inhaltlich nebeneinander stehen Einzelstudien, die selten eine Überlappung bezüglich gemeinsamer Variablen aufweisen (meist univariat angelegt); - Zusammehänge bzw. Beziehungen von Trait-Faktoren untereinander können nicht oder nur selten adäquat untersucht werden.
Tags: Faktorenanalyse, Kritik, Trait-Modell
Quelle: S116
Quelle: S116
Kartensatzinfo:
Autor: coster
Oberthema: Psychologie
Thema: Differentielle Psychologie
Schule / Uni: Universität Wien
Ort: Wien
Veröffentlicht: 08.05.2013
Tags: WS2012/13, Georg Gittler
Schlagwörter Karten:
Alle Karten (220)
16 PF (9)
Abgrenzung (1)
Adoptionsmethode (1)
Aggregation (1)
Aktivität (2)
Analysatoren (1)
Anlage/Umwelt (13)
Anwendung (4)
Army-Alpha-Test (1)
Ausdruck (1)
Beispiel (3)
Big Five (11)
Binet (5)
Carroll (2)
CAT (1)
Cattell (17)
CHC (2)
Darwin (2)
Definition (13)
EEG (2)
Einstellungstyp (1)
Entstehung (1)
Entwicklung (1)
Erblichkeit (1)
Evolution (1)
Experiment (4)
Extraversion (7)
Eysenck (14)
Faktorenanalyse (11)
Faktorenmodell (1)
Fehr (1)
Felabhängigkeit (1)
Feldabhängigkeit (2)
fMRT (1)
Forschung (22)
Fragebogen (1)
Funktionstyp (1)
Galton (3)
Gardner (3)
Geschichte (11)
Gray (1)
HAWIE (1)
Hochbegabung (4)
Hofstätter (2)
Horn (3)
Intelligenz (41)
Intelligenzmodelle (17)
Intervention (1)
Jung (6)
Kagan (1)
Kelly (4)
Korrelation (5)
Kretschmer (1)
Kritik (12)
Mendel (1)
mental Speed (3)
mental speed (1)
Merkmal (1)
Methoden (22)
Neurotizismus (3)
Normalverteilung (1)
Norman (1)
Objektivität (1)
Persönlichkeit (36)
Persönlickeit (1)
PET (1)
Prozessmodell (1)
Psychographie (2)
Psychologie (2)
Psychometrie (1)
Psychotizismus (2)
Quasi-Experiment (1)
R/S Konstrukt (4)
Rasch-Modell (17)
Reflexivität (1)
Regression (2)
Repression (2)
Rogers (7)
Sensitization (2)
Sheldon (1)
Simon-Binet-Test (1)
Skala (1)
Spearman (4)
Stabilität (1)
Stern (10)
Sternberg (6)
Stimmung (1)
Strelau (3)
Streuung (1)
Struktur (1)
Superfaktoren (1)
Terman (2)
Test (10)
Testung (1)
Theorie (6)
Thurstone (2)
TMI (3)
Trait-Modell (7)
Typenlehre (1)
Unterschiede (1)
Variable (1)
Varianz (4)
Varianzzerlegung (1)
Vernon (2)
Wahrnehmung (1)
Wechsler (2)
Witkin (1)
working memory (2)
Zuckerman (3)
Zwillingsmethode (5)



