Hol' Dir diese Lernkarten, lerne & bestehe Prüfungen. Kostenlos! Auch auf iPhone/Android!

Warum keine drei t-Tests (Depressive vs. Remittierte; Depressive vs. Gesunde; Remittierte vs. Gesunde) ?

Problem der Alphafehler-Kumulierung
Jeder statistische Test hat (selbstgewählte) Irrtumswahrscheinlichkeit: Alphafehler/Fehler 1. Art (meistens: α = 0.05)
Wenn die in Wirklichkeit gilt, wird sie (dennoch) in (nur) 5 von 100 Fällen verworfen (bei α = 0.05)

Der Alphafehler von drei t-Tests zusammen ist somit sicherlich größer als jener bloß eines (t-)Tests - Nur:Wie groß ?

Annahme: Ergebnisse der t-Tests voneinander statistisch unabhängig
Wahrscheinlichkeit für einen Alphafehler bei einem Test ist gleich α


Statistische Unabhängigkeit - Multiplikationstheorem

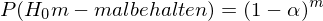
Gegenwahrscheinlichkeit: in m Tests mindestens einmal die (fälschlicherweise) verwerfen


α = 0.05, k = 3 Gruppen, m = 3 t-Tests

Der gemeinsame Fehler (familywise error) ist fast dreimal höher als der nominell gewählte.
Zuwachsrate steigt mit Anzahl der Gruppen und Vergleiche stark an:

Zudem: nicht alle Tests voneinander unabhängig reales Alpha höher!

Zur Kontrolle des familywise error können Prozeduren wie Bonferroni-Korrektur o. ä. verwendet werden - JEDOCH sehr konservatives Verfahren.

Für den simultanen Vergleich mehrerer Gruppenmittelwerte ist ANOVA somit das geeignete Analyseinstrument
– Kontrolliert den familywise error
– Ist aber nicht so konservativ wie alternative Prozeduren

Darunter versteht man den Fehler der akkumuliert wird wenn ein Test mehrfach auf eine Hypothese angewendet wird.

Warum keine drei t-Tests (Depressive vs. Remittierte; Depressive vs. Gesunde; Remittierte vs. Gesunde) ?
Problem der Alphafehler-Kumulierung
Jeder statistische Test hat (selbstgewählte) Irrtumswahrscheinlichkeit - Alphafehler/Fehler 1. Art (meistens: α = 0.05)

Beispiel:
α = 0.05, k = 3 Gruppen, m = 3 t-Tests

Der gemeinsame Fehler (familywise error) ist fast dreimal höher als der nominell gewählte.

Zur Kontrolle des familywise error können Prozeduren wie Bonferroni-Korrektur o. ä. verwendet werden.

Zur Kontrolle des familywise error können Prozeduren wie Bonferroni-Korrektur o. ä. verwendet werden.


Nachteil: Sehr konservatives Vorgehen! (Verwerfen der H0 wird u. U. unverhältnismäßig schwierig; k = 3, α = 0.05: α* = 0.017)

Für den simultanen Vergleich mehrerer Gruppenmittelwerte ist ANOVA somit das geeignete Analyseinstrument
– Kontrolliert den familywise error
– Ist aber nicht so konservativ wie alternative Prozeduren

Einfachster Fall abhängiger Daten:
2 Messungen ... t-Test für abhängige Stichproben

Test untersucht nicht wie im Fall unabhängiger Stichproben, ob sich die Mittelwerte zweier Verteilungen voneinander unterscheiden, sondern ob der Mittelwert der Differenz aller Messwertpaare ungleich 0 ist.

Abhängiger t-Test ist Test über die


Beispiel: (angelehnt an Keller et al., 2000)
Gibt es einen kombinierten Effekt bei einer Behandlung von Psychopharmaka und therapeutischer (Verhaltenstherapie – CBT) Behandlung.
Effekt einer kognitiv-behavioralen Depressionsbehandlung (CBT)
N = 56 depressive Patienten vor und nach der 12-wöchigen Behandlung

Test untersucht nicht wie im Fall unabhängiger Stichproben, ob sich die Mittelwerte zweier Verteilungen voneinander unterscheiden, sondern ob der Mittelwert der Differenz aller Messwertpaare ungleich 0 ist.

Abhängiger t-Test ist Test über die

Voraussetzungen:

1. Metrische Daten (Intervall-, Rationalskala)
2. Abhängige Messungen
3. Normalverteilung der Differenzen di

• t-Test abhängiger Stichproben: Normalverteilung muss innerhalb der berechneten  Differenzen vorhanden sein
• t-Test unabhängiger Stichproben: Normalverteilung muss in jeder der beiden Gruppen vorliegen

Beispiel: (angelehnt an Keller et al., 2000)
Effekt einer kognitiv-behavioralen Depressionsbehandlung (CBT)
N = 56 depressive Patienten vor und nach der 12-wöchigen Behandlung

Gibt es einen kombinierten Effekt bei einer Behandlung von Psychopharmaka und therapeutischer (Verhaltenstherapie – CBT) Behandlung.


Ausdruck zeigt t-Test mit abhängigen Daten: Intervention hochsignifikant wirksam
(H0 war: Differenzen unterscheiden sich nicht)

- Korrelation: Personen mit hohen Werten zu Beginn hatten auch am Ende hohe Werte.
- t-Test: t = 13, 658, Df = 55 – ist statistisch signifikant.

t-Test abhängiger Stichproben: Normalverteilung muss innerhalb der berechneten  Differenzen vorhanden sein

Zur Überprüfung der Voraussetzungen (NV) muss neue Variable berechnet werden - Messwertdifferenzen !!!

Für diese neue Variable muss die Normalverteilung überprüft werden: Diff als abhängige Variable wählen.