Hol' Dir diese Lernkarten, lerne & bestehe Prüfungen. Kostenlos! Auch auf iPhone/Android!

• Einfaktorielle Varianzanalyse (ANOVA) erlaubt simultanen Vergleich von k ≥ 2 Mittelwerten
• „Erweiterung“ des t-Test für k > 2 Gruppen

Warum keine drei t-Tests (Depressive vs. Remittierte; Depressive vs. Gesunde; Remittierte vs. Gesunde) ?
Problem der Alphafehler-Kumulierung Jeder statistische Test hat (selbstgewählte) Irrtumswahrscheinlichkeit Alphafehler/Fehler 1. Art (meistens: α = 0.05)
Der gemeinsame Fehler (familywise error) ist fast dreimal höher als der nominell gewählte. Die Zuwachsrate steigt mit Anzahl der Gruppen und Vergleiche stark an.

Für den simultanen Vergleich mehrerer Gruppenmittelwerte ist ANOVA somit das geeignete Analyseinstrument
– Kontrolliert den familywise error
– Ist aber nicht so konservativ wie alternative Prozeduren

Warum keine drei t-Tests (Depressive vs. Remittierte; Depressive vs. Gesunde; Remittierte vs. Gesunde) ?

Problem der Alphafehler-Kumulierung
Jeder statistische Test hat (selbstgewählte) Irrtumswahrscheinlichkeit: Alphafehler/Fehler 1. Art (meistens: α = 0.05)
Wenn die in Wirklichkeit gilt, wird sie (dennoch) in (nur) 5 von 100 Fällen verworfen (bei α = 0.05)

Der Alphafehler von drei t-Tests zusammen ist somit sicherlich größer als jener bloß eines (t-)Tests - Nur:Wie groß ?

Annahme: Ergebnisse der t-Tests voneinander statistisch unabhängig
Wahrscheinlichkeit für einen Alphafehler bei einem Test ist gleich α


Statistische Unabhängigkeit - Multiplikationstheorem

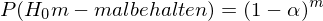
Gegenwahrscheinlichkeit: in m Tests mindestens einmal die (fälschlicherweise) verwerfen


α = 0.05, k = 3 Gruppen, m = 3 t-Tests

Der gemeinsame Fehler (familywise error) ist fast dreimal höher als der nominell gewählte.
Zuwachsrate steigt mit Anzahl der Gruppen und Vergleiche stark an:

Zudem: nicht alle Tests voneinander unabhängig reales Alpha höher!

Zur Kontrolle des familywise error können Prozeduren wie Bonferroni-Korrektur o. ä. verwendet werden - JEDOCH sehr konservatives Verfahren.

Für den simultanen Vergleich mehrerer Gruppenmittelwerte ist ANOVA somit das geeignete Analyseinstrument
– Kontrolliert den familywise error
– Ist aber nicht so konservativ wie alternative Prozeduren

Darunter versteht man den Fehler der akkumuliert wird wenn ein Test mehrfach auf eine Hypothese angewendet wird.

Warum keine drei t-Tests (Depressive vs. Remittierte; Depressive vs. Gesunde; Remittierte vs. Gesunde) ?
Problem der Alphafehler-Kumulierung
Jeder statistische Test hat (selbstgewählte) Irrtumswahrscheinlichkeit - Alphafehler/Fehler 1. Art (meistens: α = 0.05)

Beispiel:
α = 0.05, k = 3 Gruppen, m = 3 t-Tests

Der gemeinsame Fehler (familywise error) ist fast dreimal höher als der nominell gewählte.

Zur Kontrolle des familywise error können Prozeduren wie Bonferroni-Korrektur o. ä. verwendet werden.

Zur Kontrolle des familywise error können Prozeduren wie Bonferroni-Korrektur o. ä. verwendet werden.


Nachteil: Sehr konservatives Vorgehen! (Verwerfen der H0 wird u. U. unverhältnismäßig schwierig; k = 3, α = 0.05: α* = 0.017)

Für den simultanen Vergleich mehrerer Gruppenmittelwerte ist ANOVA somit das geeignete Analyseinstrument
– Kontrolliert den familywise error
– Ist aber nicht so konservativ wie alternative Prozeduren

Omnibustest
ANOVA prüft nicht sequentiell die Hypothesen
H0(1): μ1 = μ2 ; H0(2): μ1 = μ3 ; H0(3): μ2 = μ3 sondern
H0: μ1= μ2 = μ3 bzw. allgemein H0: μ1 = μ2 = … = μk

Die H1 wird angenommen, wenn sich zumindest zwei der untersuchten Mittelwerte signifikant voneinander unterscheiden


Test beruht auf einem Vergleich der Varianz der Daten, die durch
systematische Unterschiede bedingt wird (Gruppen), gegenüber der Varianz, die durch den Zufall zustande kommt → „Varianzanalyse“

Ist die Varianz der Gruppenmittelwerte um einen gemeinsamen Mittelwert größer als die Varianz innerhalb der Gruppen?
Beispiel: Depressive (rot) / Remittierte (blau) / Gesunde (grün)

Gruppenmittelwerte um einen gemeinsamen Mittelwert:

Varianz innerhalb der Gruppe:

Interpretation: die Gruppen unterscheiden sich signifikant voneinander
- H0 wird verworfen
- Welche Gruppen zeigen signifikante Unterschiede?
Einzelvergleiche (Kontraste) und Post-Hoc-Tests

Annahmen und Voraussetzungen der Varianzanalyse
Gültigkeit und Durchführung der einfaktoriellen ANOVA sind an vier Voraussetzungen gebunden:

1. Die abhängige Variable hat metrische Skaleneigenschaften (Intervallskala, Rationalskala)
2. Die Gruppen sind voneinander unabhängig
Es gibt keine Gruppe in der eine Person zweimal vorkommt
3. Die Varianzen der untersuchten Gruppen sind homogen
Varianz muss in den einzelnen Gruppen ungefähr gleich sein - Soll sich in der Varianzhomogenität zeigen
4. Die Daten sind innerhalb der Gruppen normalverteilt

Gleiche Voraussetzungen wie t-Test !
Voraussetzungen müssen vor der Durchführung geprüft werden – bei Nicht-Zutreffen u. U. anderes Testverfahren (z.B. nicht-parametrisch)

Werden Voraussetzungen nicht erfüllt kann man auf nicht-parametrische Verfahren zurückgreifen oder eventuell trotzdem auf parametrische Verfahren wenn einzelne Voraussetzungen nicht erfüllt sind (Robustheit).

Formales Modell der einfaktoriellen ANOVA

• Gesamtmittelwert und Effekt der Gruppe sind bloße Konstanten (feste Effekte [fixed effects]; Fehler haben Erwartungswert 0)
Fixed effects model: man geht von fixen Effekten in einer Gruppe aus (d.h. jede Person variiert in einer Gruppe gleich – bzw. ist ein unterschiedliches Verhalten im Fehler abgebildet)
• Fehler haben einen Erwartungswert von 0 – d.h. es wird davon ausgegangen, dass der Fehler über alle Personen hinweg in der Gruppe 0 ist, sich die Fehler also ausgleichen.
• Streuungen in der Gruppe kommen NUR durch den Fehler zustande – deshalb muss eine Varianzhomogenität gegeben sein, damit sich diese Effekt ausgleichen.
Fehler müssen sich in allen Gruppen gleich (Varianzhomogenität/Homoskedastizität) und normal verteilen
• Prüfung der Normalverteilung durch Kolmogorov-Smirnov- oder Shapiro-Wilk-Test (vgl. t-Test)

Prüfung der Normalverteilung durch Kolmogorov-Smirnov- oder Shapiro-Wilk-Test
(Notwendig als Voraussetzung z.B. für die einfaktorielle ANOVA, t-Test,...)


BDI-II-Scores bei Gesunden nicht normalverteilt (p < .05)
[H0 ist bei Voraussetzungstests „Wunschhypothese“ und soll beibehalten werden]

Box-Plots:
Verteilung bei Gesunden deutlich asymmetrisch (mehr niedrige als hohe Werte)
Keine Ausreißer

• H0: Die Verteilung ist normalverteilt. H1: Die Verteilung ist nicht normalverteilt.
• D.h. man hofft auf ein nicht signifikantes Ergebnis. Bei den Gesunden ist das Ergebnis aber signifikant – d.h. die Gesunden sind nicht normalverteilt.
• Inhaltliche Info: Durch die Art der Messung tritt der Effekt (nicht normalverteilt) auf, da nach Symptomen gefragt wird und wenn man keine Symptome hat gibt man 0 an. Aber man kann nicht weniger als 0 angeben. Deshalb ist der Verteilung eher einseitig.

Prüfung der Varianzhomogenität durch Levene-Test (= Pendant des F-Test bei k > 2 Gruppen)


p > .05, also kann Varianzhomogenität angenommen werden;
[H0 ist „Wunschhypothese“ und soll beibehalten werden]

H0 – die Varianzen sind homogen.

ANOVA ist ein robustes Verfahren, d.h. im Allgemeinen haben einzelne Voraussetzungsverletzungen keinen allzu großen Einfluss auf Ergebnis der Hypothesentestung.

a) Bei gleichen Stichprobengrößen sind Abweichungen von Normalverteilung oder der Varianzhomogenität häufig vernachlässigbar.

b) V. a. bei ungleichen ns können Abweichungen jedoch größeren Einfluss ausüben

• keine ausreichende Kontrolle von Typ-I- und Typ-II-Fehlerraten
• u. U. Ausweichen auf nicht-parametrische Tests

c) Wenn Varianzen nicht homogen

• robuster F-Test: Korrektur nach Brown-Forsythe oder Welch
• Korrigieren Freiheitsgrade des Fehlers (dfInnerhalb) und beruhen auf alternativer Berechnung der Quadratsummen

zu b) + c) Beide Prozeduren wirksam in der Kontrolle des Typ-I-Fehlers, Welch kontrolliert i. A. aber den Typ-II-Fehler besser (höhere Testmacht; vgl.
Field, 2009)


Da die ANOVA ein robustes Verfahren ist – kann die ANOVA bei diesem Beispiel trotzdem angewendet werden, auch wenn bei einer Gruppe die Normalverteilung nicht gegeben ist.
Dies ist auch abhängig  von der Stichprobengröße.
Wenn man nicht sicher ist – kann man das nicht-parametrische Verfahren anwenden und dann mit dem Ergebnis der parametrischen Verfahren zu vergleichen. Sind die Ergebnisse gleich/ähnlich so kann das parametrische Verfahren verwendet werden.

Eine Voraussetzung für die Durchführung der einfaktoriellen ANOVA ist die Varianzhomogenität.
Wenn Varianzen nicht homogen:

• robuster F-Test: Korrektur nach Brown-Forsythe oder Welch
• Korrigieren Freiheitsgrade des Fehlers (dfInnerhalb) und beruhen auf alternativer Berechnung der Quadratsummen

Aufruf in SPSS:

Ergebnis:

oben: Tabelle zur Varianzanalyse
unten: df1 = 2 Freiheitsgrade (3 Gruppen - 1)
df2 wurde von 104 nach unten korrigiert - es hat sich nicht viel geändert, da die Varianzen homogen waren

Was tun bei Verletzung? (Mauchly-Test signifikant)
... Greenhouse-Geisser- und Huynh-Feldt-Korrekturen: Bestimmung eines Faktors Epsilon zur Korrektur der Freiheitsgrade der F-Tests (Kontrolle der Typ-I-Fehlerrate)

• Greenhouse-Geisser konservativer (sicherere Variante)
• Huynh-Feldt progressiver

Wenn Korrekturen zu unterschiedlichen Ergebnissen bzgl. Verwerfung der H0 führen - ggf. Bildung eines Mittelwerts der jeweiligen p-Werte (Field, 2009, S. 476f.)


(Mixed ANOVA wie alle ANOVAs robustes Verfahren)
Sphärizität generell wichtige Voraussetzung - Empfehlung: wenn verletzt, Korrektur notwendig (ansonsten zu hohe Typ-I-Fehlerrate)

Wenn Sphärizität nicht gegeben ist, dann kann man auch eine MANOVA (multivariate ANOVA) berechnen. (wird von SPSS automatisch ausgegeben)

• Dafür darf der Box-M-Test nicht signifikant sein um die MANOVA durchzuführen: Varianz-Kovarianz-Matrizen müssen über die unabhängigen Gruppen gleich sein (p > .05)
• Nachteil: MANOVA hat im Allgemeinen eine geringere Testmacht als die mixed design ANOVA