Was bedeutet die lokale stochastische Unabhängigkeit beim RM?
Zusammenhänge zwischen den manifesten Variablen (z.B. 2 Antworten 2 verschiedener Items) sind nicht Ausdruck direkter Abhängigkeit zwischen den einzelnen Verhaltensweisen, sondern Ausdruck ihrer Abhängigkeit von einer, allen manifesten Variablen gemeinsam zugrunde liegenden latenten Dimension.
Wenn diese Betrachtung richtig ist und somit einelatente Dimension existiert, dann könnte man diese latente Dimension (statistisch) konstant halten (herauspartialisieren).
Es folgt: nach Konstanthaltung müssten die Zusammenhänge zwischen den manifesten Variablen verschwinden - lokal stochastische Unabhängigkeit
Formel:

d.h. Die Wahrscheinlichkeit, dass eine Vp mit Fähigkeit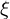 beide Items (i und j) löst ist gleich dem Produkt aus der Wahrscheinlichkeit der Einzelreaktionen, nämlich der Wahrscheinlichkeit Item i zu lösen und der Wahrscheinlichkeit Item j zu lösen. Aus der lokalen stochastischen Unabhängigkeit folgt auch insbesondere, dass die Antworten einer Person auf ein Item nicht von Antworten auf andere Items abhängen darf.
beide Items (i und j) löst ist gleich dem Produkt aus der Wahrscheinlichkeit der Einzelreaktionen, nämlich der Wahrscheinlichkeit Item i zu lösen und der Wahrscheinlichkeit Item j zu lösen. Aus der lokalen stochastischen Unabhängigkeit folgt auch insbesondere, dass die Antworten einer Person auf ein Item nicht von Antworten auf andere Items abhängen darf.
Zusätzlich wird im Rasch Modell angenommen, dass die Antworten verschiedene Personen voneinander stochastisch unabhängig sind (d.h. Schummeln verboten - beeinträchtigt die empirische Modellgeltung).
Wenn diese Betrachtung richtig ist und somit einelatente Dimension existiert, dann könnte man diese latente Dimension (statistisch) konstant halten (herauspartialisieren).
Es folgt: nach Konstanthaltung müssten die Zusammenhänge zwischen den manifesten Variablen verschwinden - lokal stochastische Unabhängigkeit
Formel:

d.h. Die Wahrscheinlichkeit, dass eine Vp mit Fähigkeit
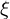 beide Items (i und j) löst ist gleich dem Produkt aus der Wahrscheinlichkeit der Einzelreaktionen, nämlich der Wahrscheinlichkeit Item i zu lösen und der Wahrscheinlichkeit Item j zu lösen. Aus der lokalen stochastischen Unabhängigkeit folgt auch insbesondere, dass die Antworten einer Person auf ein Item nicht von Antworten auf andere Items abhängen darf.
beide Items (i und j) löst ist gleich dem Produkt aus der Wahrscheinlichkeit der Einzelreaktionen, nämlich der Wahrscheinlichkeit Item i zu lösen und der Wahrscheinlichkeit Item j zu lösen. Aus der lokalen stochastischen Unabhängigkeit folgt auch insbesondere, dass die Antworten einer Person auf ein Item nicht von Antworten auf andere Items abhängen darf. Zusätzlich wird im Rasch Modell angenommen, dass die Antworten verschiedene Personen voneinander stochastisch unabhängig sind (d.h. Schummeln verboten - beeinträchtigt die empirische Modellgeltung).
Tags: lokale stochastische Unabhängigkeit, Rasch-Modell
Quelle: S44
Quelle: S44
Kartensatzinfo:
Autor: coster
Oberthema: Psychologie
Thema: Differentielle Psychologie
Schule / Uni: Universität Wien
Ort: Wien
Veröffentlicht: 08.05.2013
Tags: WS2012/13, Georg Gittler
Schlagwörter Karten:
Alle Karten (220)
16 PF (9)
Abgrenzung (1)
Adoptionsmethode (1)
Aggregation (1)
Aktivität (2)
Analysatoren (1)
Anlage/Umwelt (13)
Anwendung (4)
Army-Alpha-Test (1)
Ausdruck (1)
Beispiel (3)
Big Five (11)
Binet (5)
Carroll (2)
CAT (1)
Cattell (17)
CHC (2)
Darwin (2)
Definition (13)
EEG (2)
Einstellungstyp (1)
Entstehung (1)
Entwicklung (1)
Erblichkeit (1)
Evolution (1)
Experiment (4)
Extraversion (7)
Eysenck (14)
Faktorenanalyse (11)
Faktorenmodell (1)
Fehr (1)
Felabhängigkeit (1)
Feldabhängigkeit (2)
fMRT (1)
Forschung (22)
Fragebogen (1)
Funktionstyp (1)
Galton (3)
Gardner (3)
Geschichte (11)
Gray (1)
HAWIE (1)
Hochbegabung (4)
Hofstätter (2)
Horn (3)
Intelligenz (41)
Intelligenzmodelle (17)
Intervention (1)
Jung (6)
Kagan (1)
Kelly (4)
Korrelation (5)
Kretschmer (1)
Kritik (12)
lokale stochastische Unabhängigkeit (1)
Mendel (1)
mental Speed (3)
mental speed (1)
Merkmal (1)
Methoden (22)
Neurotizismus (3)
Normalverteilung (1)
Norman (1)
Objektivität (1)
Persönlichkeit (36)
Persönlickeit (1)
PET (1)
Prozessmodell (1)
Psychographie (2)
Psychologie (2)
Psychometrie (1)
Psychotizismus (2)
Quasi-Experiment (1)
R/S Konstrukt (4)
Rasch-Modell (17)
Reflexivität (1)
Regression (2)
Repression (2)
Rogers (7)
Sensitization (2)
Sheldon (1)
Simon-Binet-Test (1)
Skala (1)
Spearman (4)
Stabilität (1)
Stern (10)
Sternberg (6)
Stimmung (1)
Strelau (3)
Streuung (1)
Struktur (1)
Superfaktoren (1)
Terman (2)
Test (10)
Testung (1)
Theorie (6)
Thurstone (2)
TMI (3)
Trait-Modell (7)
Typenlehre (1)
Unterschiede (1)
Variable (1)
Varianz (4)
Varianzzerlegung (1)
Vernon (2)
Wahrnehmung (1)
Wechsler (2)
Witkin (1)
working memory (2)
Zuckerman (3)
Zwillingsmethode (5)



