Get these flashcards, study & pass exams. For free! Even on iPhone/Android!

– Einfaktorielle Versuchspläne
– Einzelvergleiche (Kontraste) und Post-Hoc-Tests
– Zweifaktorielle Versuchspläne – Haupteffekte & Wechselwirkungen
– Simultaner Vergleich von 2 Gruppen zu 2 Zeitpunkten (klassisches Design der Interventionsforschung) – abhängige Messungen
– (Ausblick auf) Kovarianzanalyse

• Einfaktorielle Varianzanalyse (ANOVA) erlaubt simultanen Vergleich von k ≥ 2 Mittelwerten
• „Erweiterung“ des t-Test für k > 2 Gruppen

Warum keine drei t-Tests (Depressive vs. Remittierte; Depressive vs. Gesunde; Remittierte vs. Gesunde) ?
Problem der Alphafehler-Kumulierung Jeder statistische Test hat (selbstgewählte) Irrtumswahrscheinlichkeit Alphafehler/Fehler 1. Art (meistens: α = 0.05)
Der gemeinsame Fehler (familywise error) ist fast dreimal höher als der nominell gewählte. Die Zuwachsrate steigt mit Anzahl der Gruppen und Vergleiche stark an.

Für den simultanen Vergleich mehrerer Gruppenmittelwerte ist ANOVA somit das geeignete Analyseinstrument
– Kontrolliert den familywise error
– Ist aber nicht so konservativ wie alternative Prozeduren

Warum keine drei t-Tests (Depressive vs. Remittierte; Depressive vs. Gesunde; Remittierte vs. Gesunde) ?

Problem der Alphafehler-Kumulierung
Jeder statistische Test hat (selbstgewählte) Irrtumswahrscheinlichkeit: Alphafehler/Fehler 1. Art (meistens: α = 0.05)
Wenn die in Wirklichkeit gilt, wird sie (dennoch) in (nur) 5 von 100 Fällen verworfen (bei α = 0.05)

Der Alphafehler von drei t-Tests zusammen ist somit sicherlich größer als jener bloß eines (t-)Tests - Nur:Wie groß ?

Annahme: Ergebnisse der t-Tests voneinander statistisch unabhängig
Wahrscheinlichkeit für einen Alphafehler bei einem Test ist gleich α


Statistische Unabhängigkeit - Multiplikationstheorem

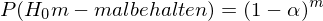
Gegenwahrscheinlichkeit: in m Tests mindestens einmal die (fälschlicherweise) verwerfen


α = 0.05, k = 3 Gruppen, m = 3 t-Tests

Der gemeinsame Fehler (familywise error) ist fast dreimal höher als der nominell gewählte.
Zuwachsrate steigt mit Anzahl der Gruppen und Vergleiche stark an:

Zudem: nicht alle Tests voneinander unabhängig reales Alpha höher!

Zur Kontrolle des familywise error können Prozeduren wie Bonferroni-Korrektur o. ä. verwendet werden - JEDOCH sehr konservatives Verfahren.

Für den simultanen Vergleich mehrerer Gruppenmittelwerte ist ANOVA somit das geeignete Analyseinstrument
– Kontrolliert den familywise error
– Ist aber nicht so konservativ wie alternative Prozeduren

Darunter versteht man den Fehler der akkumuliert wird wenn ein Test mehrfach auf eine Hypothese angewendet wird.

Warum keine drei t-Tests (Depressive vs. Remittierte; Depressive vs. Gesunde; Remittierte vs. Gesunde) ?
Problem der Alphafehler-Kumulierung
Jeder statistische Test hat (selbstgewählte) Irrtumswahrscheinlichkeit - Alphafehler/Fehler 1. Art (meistens: α = 0.05)

Beispiel:
α = 0.05, k = 3 Gruppen, m = 3 t-Tests

Der gemeinsame Fehler (familywise error) ist fast dreimal höher als der nominell gewählte.

Zur Kontrolle des familywise error können Prozeduren wie Bonferroni-Korrektur o. ä. verwendet werden.

Zur Kontrolle des familywise error können Prozeduren wie Bonferroni-Korrektur o. ä. verwendet werden.


Nachteil: Sehr konservatives Vorgehen! (Verwerfen der H0 wird u. U. unverhältnismäßig schwierig; k = 3, α = 0.05: α* = 0.017)

Für den simultanen Vergleich mehrerer Gruppenmittelwerte ist ANOVA somit das geeignete Analyseinstrument
– Kontrolliert den familywise error
– Ist aber nicht so konservativ wie alternative Prozeduren

Omnibustest
ANOVA prüft nicht sequentiell die Hypothesen
H0(1): μ1 = μ2 ; H0(2): μ1 = μ3 ; H0(3): μ2 = μ3 sondern
H0: μ1= μ2 = μ3 bzw. allgemein H0: μ1 = μ2 = … = μk

Die H1 wird angenommen, wenn sich zumindest zwei der untersuchten Mittelwerte signifikant voneinander unterscheiden


Test beruht auf einem Vergleich der Varianz der Daten, die durch
systematische Unterschiede bedingt wird (Gruppen), gegenüber der Varianz, die durch den Zufall zustande kommt → „Varianzanalyse“

Ist die Varianz der Gruppenmittelwerte um einen gemeinsamen Mittelwert größer als die Varianz innerhalb der Gruppen?
Beispiel: Depressive (rot) / Remittierte (blau) / Gesunde (grün)

Gruppenmittelwerte um einen gemeinsamen Mittelwert:

Varianz innerhalb der Gruppe:

Interpretation: die Gruppen unterscheiden sich signifikant voneinander
- H0 wird verworfen
- Welche Gruppen zeigen signifikante Unterschiede?
Einzelvergleiche (Kontraste) und Post-Hoc-Tests

• Einzelvergleiche (Kontraste)
• Post-Hoc-Tests

Einzelvergleiche häufig a priori formuliert, d.h. bereits vor Durchführung der Analyse besteht eine Hypothese, welche Mittelwerte sich voneinander unterscheiden sollten (hypothesengeleitetes Vorgehen)

Einzelvergleiche können aber auch a posteriori berechnet werden, ebenso wie Post-Hoc-Tests zur Datenexploration benutzt werden können (exploratives Vorgehen)

Einzelvergleiche = Kontraste

Erlauben spezifische Gruppenvergleiche und auch gerichtete Hypothesen z.B.: Gesunde und Remittierte haben niedrigere Werte im BDI-II als akut Depressive

Rechnerische Durchführung durch Festlegung von Linearkombinationen bzw. gewichteter Summen der Gruppenmittelwerte

• Orthogonale (= unabhängige) und nicht-orthogonale Kontraste möglich
• Allgemein:

Zwei Kontraste sind orthogonal, wenn die Summe der Produkte ihrer Koeffizienten Null ist:

Beispiel SPSS:

(Die Kontrast-Koeffizienten sind die Gewichtung. Wenn zwei Gruppen den gleichen Kontrast-Koeffizienten haben, dann werden diese zusammengelegt und gegen die andere verglichen.
Kontrast 2: Depressive sind nicht relevant – deshalb haben sie das Gewicht 0
Ergebnis der Kontrasttests ist

• Gesunde und Remittierte unterscheiden sich signifikant von Depressiven; einseitige Testung → p-Wert kann noch halbiert werden (t-Verteilung!)
• Gesunde unterscheiden sich auch signifikant von Remittierten; keine a priori Hypothese → Beibehalten des 2-seitigen p-Wertes aus SPSS

Kontraste können für sequentielle Vergleiche von Gruppenmittelwerten verwendet werden.

• Ausschluss jeweils einer Gruppe in nachfolgenden Kontrasttests (Kontrastkoeffizient = 0)
• stellt sicher, dass alle Kontraste orthogonal (= unabhängig) sind

Einseitige oder zweiseitige Testung in Kontrasten richtet sich nach dem Vorhandensein gerichteter Hypothesen

Varianzanalytische Designs zählen zu den wichtigsten Auswertungsmethoden der gesamten Statistik

• Erlauben die Untersuchung vielfältiger Fragestellungen
• Hohe Flexibilität in der Anwendung
• Allgemeines lineares Modell (ALM) hat jedoch Einschränkungen (Verteilungsannahmen, Homoskedastizität, Linearität, …)
• Erweiterungen des allgemeinen linearen Modells (ALM):
- Generalized Linear Model (GLM[GenLin]: Verteilung der abhängigen Variable kann anders als normal sein; Linearität der UV nicht zwingend notwendig)- Generalized Linear Mixed Model (GLMM/GEE: Erweiterung fester Effekte um zufällige; Modellierung unterschiedlichster abhängiger Datenstrukturen (z.B. Verletzung der Sphärizität möglich))