Warum ist die Betrachtung von Effektstärken sinnvoll? Wo werden diese eingesetzt?
- Nicht nur statistische Signifikanz für Bedeutsamkeit eines Ergebnisses ausschlaggebend
- Größe und Richtung eines Effektes (z.B. Mittelwertsunterschied, Zusammenhang) inhaltlich relevant
- APA (American Psychological Association) empfiehlt das Berichten von Effektgrößen zusätzlich zu den Ergebnissen statistischer Tests - Veranschaulichung der inhaltlichen Bedeutsamkeit eines Ergebnisses
- Im Bereich der klinischen und medizinischen Forschung sind Effektgrößen unmittelbar wichtig (Wie gut wirkt eine Behandlung? Wie groß ist der Einfluss eines Risikofaktors?)
- Effektgrößen nicht nur für Veranschaulichung von Ergebnissen wichtig
- Ebenso für Planung von Studien relevant: – Effektgröße– Alpha-Fehler– Beta-Fehler– Stichprobengrößestehen miteinander in Beziehung
- Kennt man drei der vier Parameter (oder legt sie a priori fest) kann der vierte berechnet werden - Planung von Stichprobengrößen, Ermittlung der Power einer Studie
Tags: Effektgröße
Source: VO06
Source: VO06
Welche 2 Arten von Effektgrößen können unterschieden werden? Was sind Maße für diese Effektgrößen?
Standardisierte und unstandardisierte Effektgrößen
Unstandardisierte Effektgrößen sind Maße, die eine unmittelbare inhaltliche Bedeutsamkeit und Interpretation haben, z.B.
Maße für unstandardisierte Effektgrößen z.B.
Standardisierte Effektgrößen i. A. vor allem dann von Bedeutung, wenn zugrundeliegendes Maß keine unmittelbare Interpretation gestattet, z.B. Summenwerte in psychologischen Tests und Fragebögen
Standardisierte Effektgrößen erlauben Vergleich von Ergebnissen mit Instrumenten, die unterschiedliche Skalierung haben - Unterschiede werden durch Standardisierung kompensiert
Anwendung von Effektmaßen (standardisiert, unstandardisiert) vor allem auch in meta-analytischer Forschung (= Integration von Forschungsergebnissen unterschiedlicher Studien zur selben Forschungsfrage)
Häufig verwendete standardisierte Maße
Unstandardisierte Effektgrößen sind Maße, die eine unmittelbare inhaltliche Bedeutsamkeit und Interpretation haben, z.B.
- Anzahl an Zigaretten, die im Schnitt pro Tag geraucht werden
- Krankenstandstage pro Jahr, die durchschnittlich auf einer bestimmte Erkrankung zurückgeführt werden können
- Gewichtsverlust in kg, der durch ein bestimmtes Diäts- und Aktivitätsprogramm im Schnitt erzielt werden kann
Maße für unstandardisierte Effektgrößen z.B.
- Differenz von Gruppenmittelwerten (raw mean difference)
- Unstandardisierte Regressionskoeffizienten
Standardisierte Effektgrößen i. A. vor allem dann von Bedeutung, wenn zugrundeliegendes Maß keine unmittelbare Interpretation gestattet, z.B. Summenwerte in psychologischen Tests und Fragebögen
- Summenwert u. a. abhängig von Anzahl der Items und Anzahl der Abstufungen, die zur Beantwortung eines Items vorhanden sind
- Zwei Instrumente, die dasselbe gleich gut erfassen, haben durch Unterschiede in Itemanzahl und Itemabstufungen Unterschiede in ihrer Skalierung
- Skalierungsunterschiede sind artifiziell; sagen nichts über Unterschiede in der eigentlich gemessenen Eigenschaft aus
Standardisierte Effektgrößen erlauben Vergleich von Ergebnissen mit Instrumenten, die unterschiedliche Skalierung haben - Unterschiede werden durch Standardisierung kompensiert
Anwendung von Effektmaßen (standardisiert, unstandardisiert) vor allem auch in meta-analytischer Forschung (= Integration von Forschungsergebnissen unterschiedlicher Studien zur selben Forschungsfrage)
Häufig verwendete standardisierte Maße
- Cohens d (und andere Maße der d-Familie)
- Produkt-Moment-Korrelation r (und andere Maße der r-Familie)
- Eta2 (und andere Maße der Varianzaufklärung)
- Odds Ratio und Risk Ratio (und davon abgeleitete Kennwerte)
Tags: Effektgröße
Source: VO06
Source: VO06
Was misst das Cohens d?
Standardisierte Effektgröße
Cohens d gibt den Abstand zweier Verteilungen in Einheiten ihrer
gemeinsamen Standardabweichung an
Annahmen: Normalverteilung, Homogenität der Varianzen (t-Test !!!)
- Cohens d relevant für alle Mittelwertsvergleiche zwischen zwei (unabhängigen oder abhängigen) Gruppen
- Kann aus Gruppenmittelwerten, Standardabweichungen und ns oder aus der t-Statistik des t-Test berechnet werden (wird nicht von SPSS ausgegeben)
Cohens d gibt den Abstand zweier Verteilungen in Einheiten ihrer
gemeinsamen Standardabweichung an
Annahmen: Normalverteilung, Homogenität der Varianzen (t-Test !!!)
Tags: Cohens d, Effektgröße
Source: VO06
Source: VO06
Was sind die Annahmen für Cohens d?
Wie wird Cohens d für abhängige bzw. unabhängige Stichproben berechnet?
Wie wird Cohens d für abhängige bzw. unabhängige Stichproben berechnet?
Annahmen: Normalverteilung, Homogenität der Varianzen (t-Test !!!)
Cohens d gibt den Abstand zweier Verteilungen in Einheiten ihrer
gemeinsamen Standardabweichung an
Cohens d gibt den Abstand zweier Verteilungen in Einheiten ihrer
gemeinsamen Standardabweichung an
Tags: Cohens d, Effektgröße
Source: VO06
Source: VO06
Wann spricht man bei Cohens d von einem kleinen, mittleren oder großen Effekt?
Faustregeln und Richtlinien zur Einschätzung der Größe eines Effekts (Cohen, 1988)
Tags: Cohens d, Effektgröße
Source: VO06
Source: VO06
Wie erfolgt die Berechnung des Cohens d für folgendes Beispiel - Welche Berechnungsschritte sind notwendig?
- Was bedeutet ein Ergebnis vom Cohens d von 1.83?
- Was bedeutet ein Ergebnis vom Cohens d von 1.83?
Standardabweichung wird auf das gleiche Maß gebracht und diese werden dann verglichen.
Analyse (t-Test für abhängige Daten) hat gezeigt, dass Veränderung hochsignifikant war – Größe des Effekts?
- Unserer Effekt war signifikant – aber wie groß ist denn der Effekt?
- Korrelation von 0,66 – Pre- und Post-Testwerte
- T-Wert und N wird zur Berechnung noch benötigt.
Dann muss die Berechnung des Cohens d manuell durchgeführt werden (in SPSS ist das Cohens d nicht implementiert.)
1,83 – sehr großer Effekt / auch 1,51 ist noch ein sehr großer Effekt.
Um keine Über – oder Unterschätzungen von Effekten zu haben, sollte die Formel mit den unabhängigen Designs verwendet werden.
Analyse (t-Test für abhängige Daten) hat gezeigt, dass Veränderung hochsignifikant war – Größe des Effekts?
- Unserer Effekt war signifikant – aber wie groß ist denn der Effekt?
- Korrelation von 0,66 – Pre- und Post-Testwerte
- T-Wert und N wird zur Berechnung noch benötigt.
Dann muss die Berechnung des Cohens d manuell durchgeführt werden (in SPSS ist das Cohens d nicht implementiert.)
1,83 – sehr großer Effekt / auch 1,51 ist noch ein sehr großer Effekt.
Um keine Über – oder Unterschätzungen von Effekten zu haben, sollte die Formel mit den unabhängigen Designs verwendet werden.
Tags: Cohens d, Effektgröße
Source: VO06
Source: VO06
Welchen Einfluss hat r auf die Berechnung des Cohens d?
Wenn r > .5, ist d der Differenzwerte größer als d in Metrik unabhängiger Stichproben (bei r = .5 idente Ergebnisse; ansonsten kleiner)
Beispiel:
In Messwiederholungsdesigns sollte d in der Metrik unabhängiger Stichproben berechnet werden (vgl. Dunlap et al., 1996) ansonsten droht Über- oder Unterschätzung von Effekten und Vergleiche mit Untersuchungen mit unabhängigen Designs (VG vs. KG) werden erschwert
Beispiel:
In Messwiederholungsdesigns sollte d in der Metrik unabhängiger Stichproben berechnet werden (vgl. Dunlap et al., 1996) ansonsten droht Über- oder Unterschätzung von Effekten und Vergleiche mit Untersuchungen mit unabhängigen Designs (VG vs. KG) werden erschwert
Tags: Cohens d, Effektgröße
Source: VO06
Source: VO06
Welche anderen Indizes werden ähnlich berechnet wie Cohens d?
Neben Cohens d existieren noch weitere verwandte Indizes, die ähnlich berechnet werden: z.B. Hedges g, Glass Δ.
- Cohens d vermutlich am meisten verwendet
- Cohens d vermutlich am meisten verwendet
Tags: Cohens d, Effektgröße
Source: VO06
Source: VO06
Was ist das Effektmaß Produkt-Moment-Korrelation r? Was sind Anforderungen an die Daten?
- Produkt-Moment-Korrelation r ist bereits selbst ein standardisiertes Effektmaß
- Wertebereich auf −1 bis +1 beschränkt
- Zeigt Richtung des Effekts an
- Erlaubt Aussagen über das Ausmaß erklärter Varianz (= Bestimmtheitsmaß r2 [ebenso für Regression von Bedeutung, R2])
- Weitere Koeffizienten aus der r-Familie sind Phi-Koeffizient, die punktbiseriale Korrelation und die Rangkorrelation - Cave: Einschränkungen des Koeffizienten (siehe z.B. Phi-Koeffizient) schlagen sich auch auf Einschätzung der Größe eines Effekts nieder
- Alle diese Koeffizienten können (prinzipiell) als Effektmaße verwendet und verstanden werden
- Auch die Produkt-Moment-Korrelation stellt Anforderungen an Daten: bivariate Normalverteilung, linearer Zusammenhang
Tags: Effektgröße, Produkt-Moment-Korrelation, r
Source: VO06
Source: VO06
Wie ist der Zusammenhang zwischen r und d?
r kann zudem in Cohens d umgerechnet werden und umgekehrt
Korrelative Herangehensweise und die Analyse von Mittelwertsunterschieden im allgemeinen linearen Modell (ALM) eigentlich dasselbe
(Hintergrund: Korrelationen (Zusammenhangshypothese) können als Mittelwertsunterschiede (Unterschiedshypothese) formuliert werden und umgekehrt)
Korrelative Herangehensweise und die Analyse von Mittelwertsunterschieden im allgemeinen linearen Modell (ALM) eigentlich dasselbe
(Hintergrund: Korrelationen (Zusammenhangshypothese) können als Mittelwertsunterschiede (Unterschiedshypothese) formuliert werden und umgekehrt)
Tags: Cohens d, Effektgröße, r
Source: VO06
Source: VO06
Wann spricht man bei r von einem kleinen, mittleren oder großen Effekt?
Faustregeln und Richtlinien zur Einschätzung der Größe eines Effekts: Cohen (1988), Lipsey und Wilson (2001)
- Lipsey und Wilson (2001) argumentieren, dass Angaben Cohens nicht korrekt - Umrechnung von d nach r ergibt Benchmarks von .10, .24, .37
- Um konsistent zu sein, können auch schon kleinere Koeffizienten als von Cohen angenommen für mittlere und große Effekte stehen
Tags: Cohens d, Effektgröße, r
Source: VO06
Source: VO06
Was ist das Effektmaß 
?
?- Eta2 (
) ist das „natürliche“ Effektmaß varianzanalytischer Untersuchungen - Eta2 ist ein Maß dafür, wie viel Gesamtvarianz der abhängigen Variable durch den interessierenden Faktor (= unabhängige Variable) erklärt wird:
- Ergebnis ist ein Maß der Varianzaufklärung (Wertebereich 0 bis 1), das in der Interpretation vergleichbar ist mit r2
- Eta2 ist ein Globalmaß für Gesamteffekt eines Faktorsoder einer Wechselwirkung
- Auch gerade bei varianzanalytischen Designs ist jedoch häufig die Bestimmung des Unterschiedes spezifischer Gruppen informativer - D.h. zusätzlich zu Eta2 können/sollten in varianzanalytischen Designs auch andere Effektgrößen (z.B. Cohens d) bestimmt werden
Tags: Effektgröße, Eta
Source: VO07
Source: VO07
Was ist das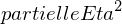 
? Wie ist der Zusammenhang zu ?
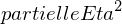? Wie ist der Zusammenhang zu ?Für mehrfaktorielle Designs wird auch das partielle Eta2 verwendet:
- Partielles Eta2 ist ein Maß der Varianzaufklärung unter Kontrolle (Herauspartialisierung) des Einflusses aller anderen Faktoren in der Gesamtvariabilität
- Wird von SPSS ausgegeben
- In einfaktoriellen Designs gilt: Eta2 = partielles Eta2
- In mehrfaktoriellen Designs gilt meist: Eta2 < partielles Eta2
- Interpretation als Maß der Varianzaufklärung bei partiellem Eta2 problematisch - Addiert man in mehrfaktoriellen Designs die partiellen Eta2 aller Faktoren und Wechselwirkungen kann die Summe > 1 (Varianzaufklärung > 100%) sein- Faktoren erklären scheinbar mehr Varianz als vorhanden ist
- Empfehlung, statt partiellem Eta2 lediglich Eta2 zu benutzen und zu berichten, da dies weniger verzerrt - Berechnung mit der Hand
Tags: Effektgröße, partielle Eta
Source: VO07
Source: VO07
Wie kann bei einer mixed ANOVA berechnet werden?
berechnet werden?In mixed design ANOVA gibt es zwei Fehlerterme (QSFehler für ZSF, QSRes für ISF und Wechselwirkung)
Berechnung von (partiellem) Eta2 getrennt für unabhängigen und abhängigen Faktor
Berechnung von (partiellem) Eta2 getrennt für unabhängigen und abhängigen Faktor
- Eta2 ein deskriptives Maß
- Statt Eta2 (= erklärte Varianz in der Stichprobe) wird deshalb häufiger auch vorgeschlagen, ω2 (Omega2 = Schätzer der erklärten Varianz in der Population) zu berechnen
Tags: Effektgröße, Eta, mixed ANOVA, partielle Eta
Source: VO07
Source: VO07
Wie können Effektgrößen für Kontraste berechnet werden?
Einerseits direkt über die entsprechenden QS (polynomiale Kontraste)
Andererseits auch über t- oder F-Werte der Kontrasttests (vgl. Field, 2009, S. 390, S. 532)
Quadrieren des oben erhaltenen Wertes erlaubt Angabe der erklärten Varianz (Cave:
= 
in diesem Fall !)
Andererseits auch über t- oder F-Werte der Kontrasttests (vgl. Field, 2009, S. 390, S. 532)
Quadrieren des oben erhaltenen Wertes erlaubt Angabe der erklärten Varianz (Cave:
= in diesem Fall !)Tags: Effektgröße, partielle Eta, r
Source: VO07
Source: VO07
Tags: Effektgröße, Eta
Source: VO07
Source: VO07
Was zeigt dieser SPSS-Ausdruck?
Effektstärken: Wie groß sind Effekte der Kontraste (Depressive vs. Remittierte & Gesunde, Remittierte vs. Gesunde; polynomiale Kontraste)?
Der Faktor Gruppe erklärt 65% der Gesamtvarianz
Im einfaktoriellen Design gilt: partielles Eta2 = Eta2.
Der Faktor Gruppe erklärt 65% der Gesamtvarianz
Im einfaktoriellen Design gilt: partielles Eta2 = Eta2.
Tags: Effektgröße, Eta, SPSS
Source: VO07
Source: VO07
Was sind die Effektgrößen für polynomiale Kontraste?
a) linearer Term?
b) quadratischer Term?
a) linearer Term?
b) quadratischer Term?
(gewichtete QS verwenden)
Linearer Term: Eta2 = 12082.501 / 19673.514 = .61
Quadratischer Term: Eta2 = 734.649 / 19673.514 = .04
Der Anteil der linearen Komponente ist 61%, jener der quadratischen 4% ergibt zusammen die 65% Varianzaufklärung des Faktors.
Polynomiale Komponenten sind orthogonal ... daher addieren sie sich zu Gesamteffekt des Faktors (dies sieht man im SPSS Ausdruck)
Linearer Term: Eta2 = 12082.501 / 19673.514 = .61
Quadratischer Term: Eta2 = 734.649 / 19673.514 = .04
Der Anteil der linearen Komponente ist 61%, jener der quadratischen 4% ergibt zusammen die 65% Varianzaufklärung des Faktors.
Polynomiale Komponenten sind orthogonal ... daher addieren sie sich zu Gesamteffekt des Faktors (dies sieht man im SPSS Ausdruck)
Tags: Effektgröße, Eta
Source: VO07
Source: VO07
Wie groß ist der Anteil an Varianz in Trait-Angst, der auf das Geschlecht, wie hoch jener, der auf das Vorliegen einer Angsterkrankung zurückgeführt werden kann?
Interpretiere es auf Basis dieses SPSS-Ausdrucks:
Interpretiere es auf Basis dieses SPSS-Ausdrucks:
- Partielles Eta2: Geschlecht erklärt 6% der Varianz, Gruppe 48%, Wechselwirkung < 1%
- Eta2 : QSTotal = QSGeschlecht + QSGruppe + QSGeschlecht * Gruppe + QSFehler = 21822.335(es wird die Gesamtvarianz berechnet und dann jeweils manuell die Varianz für jeden einzelnen Faktor)
- Geschlecht 3%, Gruppe 47%, Wechselwirkung < 1%
- Einfluss des Geschlechts tatsächlich nur halb so groß, verglichen mit partiellem Eta2 (Dass Eta2 ist kleiner als das partielle Eta2. Um einen Schätzer der Varianzerklärung zu erhalten soll Eta2 verwendet werden, damit es nicht zu einer Überschätzung kommt.)
Tags: Effektgröße, Eta, partielle Eta, SPSS
Source: VO07
Source: VO07
Zur Frage:
Wie groß sind Prä/Post-Differenzen, wie stark unterscheiden sich die Gruppen zu T1 und T2?
Was muss untersucht werden?
Was zeigen die SPSS Ausdrucke?
Betrachtet werden Eta2 als auch Cohens d.
Zu 1. SPSS Ausdruck - Tests der Innersubjekteffekte:
Partielles Eta2: addiert sich nicht auf 100% (> 100%) !
Zeit 87% der Varianz, Wechselwirkung 32%
Eta2 :
QSTotal_Innersubjekt = QSZeit + QSZeit * Behandlung + QSFehler(Zeit) = 11873.699
Zeit 82%, Wechselwirkung 6% (Wenn man auf die Partialisierung verzichtet hat man nur mehr ein Fünftel des Effekts!)
Zu 2. SPSS Ausdruck - Tests der Zwischensubjekteffekte:
Partielles Eta2: Behandlung 3% der Varianz
Eta2 :
QSTotal_Zwischensubjekt = QSBehandlung + QSFehler = 6012.600
Behandlung 3%
Partielles Eta2 und Eta2 sind hier wieder ident (nur ein Faktor in den Zwischensubjekteffekten)
Cohens d (berechnet mittels t-Tests):
Um die Effektivität der beiden Behandlungsarten im Pre-Post zu betrachten. Cohens d ist anschaulicher als Eta.
Effekt Prä/Post in CBT + Med deutlich größer als in CBT allein
Zu 1. SPSS Ausdruck - Tests der Innersubjekteffekte:
Partielles Eta2: addiert sich nicht auf 100% (> 100%) !
Zeit 87% der Varianz, Wechselwirkung 32%
Eta2 :
QSTotal_Innersubjekt = QSZeit + QSZeit * Behandlung + QSFehler(Zeit) = 11873.699
Zeit 82%, Wechselwirkung 6% (Wenn man auf die Partialisierung verzichtet hat man nur mehr ein Fünftel des Effekts!)
Zu 2. SPSS Ausdruck - Tests der Zwischensubjekteffekte:
Partielles Eta2: Behandlung 3% der Varianz
Eta2 :
QSTotal_Zwischensubjekt = QSBehandlung + QSFehler = 6012.600
Behandlung 3%
Partielles Eta2 und Eta2 sind hier wieder ident (nur ein Faktor in den Zwischensubjekteffekten)
Cohens d (berechnet mittels t-Tests):
Um die Effektivität der beiden Behandlungsarten im Pre-Post zu betrachten. Cohens d ist anschaulicher als Eta.
- Baseline-Testung CBT vs. CBT + Med: d = -0.37 (p = .057)
- Post-Testung CBT vs. CBT + Med: d = 0.78 (p < .001)
- CBT Prä/Post: d = 1.51 (p < .001) (Starker Effekt)
- CBT + Med Prä/Post: d = 2.74 (p < .001) (fast um 3-fache Standardabweichung besseres Ergebnis)
Effekt Prä/Post in CBT + Med deutlich größer als in CBT allein
Tags: Cohens d, Effektgröße, Eta, partielle Eta
Source: VO07
Source: VO07
Inwiefern können OR und RR als Effektmaße verwendet werden?
Inwiefern können diese in andere Effektmaße überführt werden?
Inwiefern können diese in andere Effektmaße überführt werden?
- OR und RR können ebenfalls als Effektmaße herangezogen werden
- Sie erlauben direkte Quantifizierung der Größe von Zusammenhängen und sind auch direkt anschaulich
- OR: Faktor, um den sich die Chancen eines Ereignisses in einer Gruppe gegenüber einer anderen Gruppe erhöhen/erniedrigen
- RR: Faktor, um den die Auftrittswahrscheinlichkeit (Inzidenz) eines Ereignisses durch Vorhandensein eines Risikofaktors erhöht/erniedrigt wird
- d, r und OR können ineinander umgerechnet werden - Anschaulichmachung kleiner/mittlerer/großer Effekte
OR und d
- Faustregeln zur Einschätzung der Größe eines Effekts (Cohen, 1988) gemäß der Umrechnung von d zu OR
- Referenzwerte nur für dichotome Variablen gut anwendbar
- In logistischer Regression ist ebenso OR das Zusammenhangs- und Effektmaß - obige Referenzwerte sind für kontinuierliche Prädiktoren nicht geeignet
RR und NNT
- RR kann nicht wie OR umgerechnet werden Eine damit zusammenhängende Effektgröße ist aber Number Needed to Treat (NNT; Anzahl der notwendigen Behandlungen)
- NNT = Anzahl jener Patienten, die mit Behandlung A behandelt werden müssen, damit gegenüber Behandlung B ein Patient mehr das gewünschte Therapieziel erreicht (komparative Maßzahl)
Tags: Cohens d, Effektgröße, NNT, odds ratio, risk ratio
Source: VO07
Source: VO07
Was ist NNT? Wertebereich? Wie wird diese berechnet?
- Eine mit dem risk ratio zusammenhängende Effektgröße ist Number Needed to Treat (NNT; Anzahl der notwendigen Behandlungen)
- Wichtige Kennzahl in der klinischen und Interventionsforschung
- Quantifiziert Überlegenheit einer Behandlung A (Testbehandlung) gegenüber einer Behandlung B (Kontrollbehandlung)
- NNT = Anzahl jener Patienten, die mit Behandlung A behandelt werden müssen, damit gegenüber Behandlung B ein Patient mehr das gewünschte Therapieziel erreicht (komparative Maßzahl)
Wertebereich
- Wertebereich der NNT von 1 bis unendlich - Sind Behandlung A und B (nahezu) gleichwertig - NNT große Zahl(Man muss unendliche viele Leute behandeln, damit eine Person das gewünschte Therapieziel erreicht).- Ist Behandlung A besser als B NNT kleine Zahl- Wenn Kontrollbehandlung besser als Testbehandlung NNT < 0 NNT < 0: Number Needed to Harm (NNH)... wird mit positivem Vorzeichen versehen (NNH = −NNT, wenn NNT < 0)... Wertebereich der NNH wiederum von 1 bis unendlich
Berechnung
- Berechnung der NNT über die sog. absolute Risikoreduktion (ARR; absolute risk reduction)
- NNT wird berechnet:
- NNT wird üblicherweise aufgerundet, wenn nicht ganzzahlig (ansonsten Überschätzung des Effekts)
- ARR > 0 Behandlung A ist besser- ARR < 0 Behandlung B ist besser
Wenn ARR < 0 (Kontrollbehandlung besser als Testbehandlung) .... NNH = −NNTTags: Effektgröße, NNT
Source: VO07
Source: VO07
Was bedeutet ein Ergebnis für NNT von 3 für dieses Beispiel:
Was muss bei einer Interpretation von NNT beachtet werden?
Was muss bei einer Interpretation von NNT beachtet werden?
Hintergrund - Berechnung NNT:
Inhaltliche Interpretation:
Inhaltliche Interpretation:
- Bereits ab 3 Patienten, die mit CBT + Med (Behandlung A) behandelt werden, profitiert schon ein Patient mehr von dieser Behandlung, verglichen mit der reinen CBT-Behandlung (Behandlung B) großer Effekt der Behandlung A gegenüber B (NNT sehr klein)
- Generell hängt Interpretation der NNT von der Art der Störung oder Erkrankung und den verglichenen Behandlungen ab (vgl. McQuay & Moore, 1997)
- NNT ist damit deskriptive Maßzahl für den Vergleich zweier spezifischer Methoden im Hinblick auf ein spezifisches interessierendes Ereignis (Outcome) nicht uneingeschränkt über beliebige Untersuchungen vergleichbar!
Tags: Effektgröße, NNT
Source: VO07
Source: VO07
Wofür spielt die Spezifizierung der Größe von Effekten eine wichtige Rolle?
Spezifizierung der Größe von Effekten wichtig für die Planung (prospektiv) und zur Einschätzung der methodischen Güte (post hoc) von Studien - Festlegung eines N, das zum statistisch signifikanten Nachweis eines Effekts bestimmter Größe benötigt wird.
Tags: Effektgröße, Planung, Signifikanz
Source: VO07
Source: VO07
Was bedeutete diese Grafik:
Wie können die einzelnen Parameter festgelegt werden?
Wie können die einzelnen Parameter festgelegt werden?
Zusammenhang zwischen den einzelnen Parameter.
Kennt man 3 der 4 Parameter (oder legt sie fest), kann der 4. berechnet werden.
Festgelegt werden zur Ermittlung von N
Signifikanzniveau wird festgelegt basierend auf der Hypothese. (Häufig: 1% oder 5%)
Testmacht
Größe des Effekts kann üblicherweise
Festlegung der Effektgröße macht aus einer ansonsten unspezifischen H1 eine spezifische H1.
Um eine spezifische H1 bestmöglich (d.h. mit bekannter Power) zu testen, kann ein optimaler Stichprobenumfang bestimmt werden hilfreich für die Planung jeder empirischen Studie.
Bestimmung optimaler Stichprobenumfänge mithilfe von Tabellen (z.B. Bortz & Döring, 2002) oder Formeln (z.B. Bortz, 2008)
Kennt man 3 der 4 Parameter (oder legt sie fest), kann der 4. berechnet werden.
Festgelegt werden zur Ermittlung von N
- Signifikanzniveau (plus Entscheidung: einseitig/zweiseitig)
- Testmacht
- Effektgröße
Signifikanzniveau wird festgelegt basierend auf der Hypothese. (Häufig: 1% oder 5%)
Testmacht
- Wahrscheinlichkeit, dass H0 verworfen wird, wenn sie nicht gilt
- = 1 − β; β = Fehler 2. Art = Wahrscheinlichkeit, dass H0 nicht verworfen wird, obwohl sie in der Population nicht gilt
- Testmacht wird üblicherweise mit .80 festgelegt (vgl. Cohen, 1988: α : β = 1 : 4; wenn α = .05 β = .20 1 − β = .80)
Größe des Effekts kann üblicherweise
- inhaltlich begründet festgelegt werden
- aus Vorstudien erschlossen werden
- anhand konventioneller Cutoffs festgelegt werden (z.B. Cutoffs von Cohen): z.B. im Rahmen der Forschung zu psychologischen Interventionen ist die Annahme eines großen Behandlungseffektes (d » 0.8) häufig angemessen
Festlegung der Effektgröße macht aus einer ansonsten unspezifischen H1 eine spezifische H1.
Um eine spezifische H1 bestmöglich (d.h. mit bekannter Power) zu testen, kann ein optimaler Stichprobenumfang bestimmt werden hilfreich für die Planung jeder empirischen Studie.
Bestimmung optimaler Stichprobenumfänge mithilfe von Tabellen (z.B. Bortz & Döring, 2002) oder Formeln (z.B. Bortz, 2008)
- Direkt anwendbar für alle möglichen Analysearten (z.B. t-Test, ANOVA, Korrelation, Regression, etc.)
- Empfehlenswertes frei verfügbares Programm: G*Power
Tags: Effektgröße, Optimaler Stichprobenumfang, Signifikanz, Testmacht
Source: VO07
Source: VO07
Wie ist der Zusammenhang zwischen N und Effektgröße (bei fixer Signfikanz und Testmacht)?
α = .05 einseitig / Testmacht 1 − β = .80
Benötigtes n pro Gruppe, um einen Effekt gewählter Größe mit einer Testmacht von 80% und bei einseitiger Testung mit einer Fehlerwahrscheinlichkeit von 5% statistisch signifikant nachweisen zu können.
Benötigtes n pro Gruppe, um einen Effekt gewählter Größe mit einer Testmacht von 80% und bei einseitiger Testung mit einer Fehlerwahrscheinlichkeit von 5% statistisch signifikant nachweisen zu können.
Tags: Effektgröße, Optimaler Stichprobenumfang, Stichprobe
Source: VO07
Source: VO07
Was ist der Zusammenhang zwischen der Stichprobengröße (N) und das Verwerfen der H0?
Wechselseitige Zusammenhänge zwischen N, Power, Effektgröße und Signifikanzniveau veranschaulichen noch ein weiteres Phänomen:
Mit steigendem N wird jede beliebige H0 mit Sicherheit verworfen
Veranschaulichung Zusammenhang N und p
Bsp.: Mittelwertsvergleich, t-Test für unabhängige Stichproben
M1= 100, M2 = 105, SDpooled = 25
...kleiner Effekt (d = 0.2)
Ist inhaltliche Interpretation, dass Effekt von d = 0.2 im gegebenen Fall bedeutsam, dann sind Studien dieser Größe schlicht zu klein und underpowered, um ihn zu belegen.
Unterste zwei Zeilen:
Ist inhaltliche Interpretation, dass Effekt von d = 0.2 im gegebenen Fall unbedeutend, dann erbringen Studien dieser Größe irrelevante signifikante Ergebnisse.
Mit steigendem N wird jede beliebige H0 mit Sicherheit verworfen
- Ist Stichprobe groß genug, kann jeder beliebig kleine Effekt signifikant werden
- Andererseits: selbst wenn ein Effekt existiert, kann die Stichprobe schlicht zu klein sein, um Signifikanz erreichen zu können underpowered study
- Verwerfen der H0 bedeutet nicht unbedingt, dass ein bedeutsamer Effekt gefunden wurde
- Beibehalten der H0 bedeutet nicht unbedingt, dass kein Effekt existiert
Veranschaulichung Zusammenhang N und p
Bsp.: Mittelwertsvergleich, t-Test für unabhängige Stichproben
M1= 100, M2 = 105, SDpooled = 25
...kleiner Effekt (d = 0.2)
Ist inhaltliche Interpretation, dass Effekt von d = 0.2 im gegebenen Fall bedeutsam, dann sind Studien dieser Größe schlicht zu klein und underpowered, um ihn zu belegen.
Unterste zwei Zeilen:
Ist inhaltliche Interpretation, dass Effekt von d = 0.2 im gegebenen Fall unbedeutend, dann erbringen Studien dieser Größe irrelevante signifikante Ergebnisse.
Tags: Effektgröße, Optimaler Stichprobenumfang, Signifikanz, Stichprobe
Source: VO08
Source: VO08
Inwiefern hilft die Effektgröße hinsichtlich des korrekten Verwerfens bzw. Beibehalten der H0?
Verwendung von Effektgrößen hilft
Wichtig: Eine Einschätzung von Effektgrößen ist keine willkürliche, sondern soll empirisch betrieben werden (gut begründen)
- inhaltlich unbedeutende Effekte (trotz ihrer möglichen Signifikanz) als solche zu erkennen
- Hinweise auf das Vorliegen hypothesenkonformer Effekte zu erhalten, selbst wenn Studie möglicherweise underpowered war (nicht-signifikantes Ergebnis)
Wichtig: Eine Einschätzung von Effektgrößen ist keine willkürliche, sondern soll empirisch betrieben werden (gut begründen)
Tags: Effektgröße, Signifikanz
Source: VO08
Source: VO08
Welche Möglichkeiten (3) gibt es zur Berechnung der Effektgröße für den U-Test?
Für U-Test existiert keine eigenständige Definition einer Effektgröße
Allerdings:
Allerdings:
- Berechnung und Angabe des sog. relativen Effekts mithilfe der mittleren Rangsummen (Mann & Whitney, 1947)
- Maßzahl der stochastischen Tendenz interpretierbar als Wahrscheinlichkeit, dass eine Person aus Gruppe 2 einen höherer Wert als eine Person aus Gruppe 1 hat
- Weitere Möglichkeit über asymptotische Eigenschaften von U: Verteilung von U kann mithilfe von z-Verteilung (Standardnormalverteilung) approximiert werden - approximative Bestimmung der Effektgröße r
Tags: Effektgröße, nicht-parametrische Verfahren, U-Test
Source: VO09
Source: VO09
Wie lässt sich bei einem Kruska-Wallis-Test (H-Test) der familywise error kontrollieren? Beschreibe diese.
Familywise error wird implizit (Kontraste) oder explizit (Post-Hoc-Tests) kontrolliert.
Kontraste
Berechnung der kritischen Differenzen
Durch Verwendung von
wird eine implizite Fehlerkontrolle angewandt - familywise error bleibt auf gewähltem α-Niveau
Post-Hoc-Tests:
2 äquivalente Methoden:
Explizite Fehlerkontrolle: Bonferroni-Korrektur als einfachste Methode:
Kritische Differenzen nach Siegel und Castellan mit expliziter
Fehlerkontrolle
Größe der kritischen Differenzen (implizite/explizite Fehlerkontrolle) abhängig von der Größe der verglichenen Stichproben (= Nj)
Sind Stichproben nicht gleich groß, müssen für jeden Vergleich unterschiedliche kritische Differenzen bestimmt werden
Kontraste
Berechnung der kritischen Differenzen
Durch Verwendung von
wird eine implizite Fehlerkontrolle angewandt - familywise error bleibt auf gewähltem α-NiveauPost-Hoc-Tests:
2 äquivalente Methoden:
- Testung aller interessierenden (!) Vergleiche mittels U-Tests
- Bestimmung der kritischen Differenzen nach Siegel und Castellan (1988)
Explizite Fehlerkontrolle: Bonferroni-Korrektur als einfachste Methode:
- Werden alle k Gruppen miteinander verglichen, kann α* sehr niedrig und die Testung damit sehr konservativ werden !
- A priori Auswahl und Beschränkung auf jene Vergleiche, die von Interesse sind - m‘ (= Anzahl dieser Vergleiche) ist dann kleiner als m und Testung damit weniger konservativ
Kritische Differenzen nach Siegel und Castellan mit expliziter
Fehlerkontrolle
-
ist kritischer z-Wert von α* - kann aus Tabellen abgelesen werden - Vorgehen ist äquivalent zur Anwendung sequentieller U-Tests
Größe der kritischen Differenzen (implizite/explizite Fehlerkontrolle) abhängig von der Größe der verglichenen Stichproben (= Nj)
Sind Stichproben nicht gleich groß, müssen für jeden Vergleich unterschiedliche kritische Differenzen bestimmt werden
Tags: Effektgröße, H-Test, Kontrast, Kruska-Wallis-Test, Post-Hoc-Test
Source: VO10
Source: VO10
Wie kann man die relativen Effekte bei diesem Beispiel interpretieren?
Gesunde haben die niedrigste Wahrscheinlichkeit höhere Werte als alle anderen aufzuweisen, Depressive haben die höchste Wahrscheinlichkeit
Tags: Effektgröße, H-Test, Kruska-Wallis-Test, nicht-parametrische Verfahren
Source: VO10
Source: VO10
Flashcard set info:
Author: coster
Main topic: Psychologie
Topic: Statistik
School / Univ.: Universität Wien
City: Wien
Published: 21.06.2013
Card tags:
All cards (175)
4-Felder-Tafel (17)
abhängige Daten (6)
ALM (1)
ANCOVA (3)
ANOVA (15)
Bindung (1)
Cohens d (10)
Cohens Kappa (6)
Effektgröße (31)
Einzelvergleich (2)
Einzelvergleiche (1)
Eta (7)
Fehler (1)
Friedman-Test (3)
H-Test (5)
Haupteffekt (2)
Haupteffekte (1)
Interaktion (5)
Konkordanz (4)
Kontrast (11)
Kontrollvariable (1)
MANOVA (2)
McNemar-Test (4)
Mediantest (5)
Medientest (1)
mixed ANOVA (10)
NNT (3)
Normalverteilung (3)
NPV (4)
Nulldifferenzen (1)
odds ratio (7)
partielle Eta (5)
phi-Koeffizient (1)
Phi-Koeffizienz (1)
Planung (1)
Post-Hoc-Test (4)
Post-hoc-Tests (3)
Power (1)
PPV (4)
Prävalenz (6)
r (4)
Reliabilität (1)
risk ratio (7)
Sensitivität (6)
Signifikanz (6)
Spezifität (6)
Sphärizität (2)
SPSS (14)
SPss (1)
Stichprobe (3)
Störvariable (1)
t-Test (7)
Testmacht (2)
Trends (1)
U-Test (6)
Varianz (2)
Varianzanalyse (11)
Varianzschätzer (1)
Voraussetzungen (2)
Vorzeichentest (2)
Wechselwirkung (3)
Wilcoxon-Test (4)
x2-Test (5)
