Wann sollen nicht-parametrische Verfahren eingesetzt werden?
Parametrische Verfahren (z.B. F-Test, t-Test, ANOVA) wichtigste statistische Methoden der empirischen Forschung - aber haben Voraussetzungen
Nicht-parametrische Verfahren sind hingegen i. d. R. voraussetzungsärmer
- Parametrische Verfahren eignen sich aber nicht für alle Daten - Skalenniveau der abhängige Variable (AV) muss metrisch sein
- Stellen Anforderungen an die Verteilung und einzelne Parameter der Daten („parametrische Verfahren“); typischerweise: - Normalverteilung- Varianzhomogenität
- Voraussetzungsverletzungen können Typ-I- und Typ-II-Fehlerhäufigkeiten beeinflussen
Nicht-parametrische Verfahren sind hingegen i. d. R. voraussetzungsärmer
- Benötigen nicht unbedingt metrische Daten
- Kommen häufig ohne Annahmen zur Verteilung aus
- Mathematische Grundlage nicht-parametrischer Verfahren aber heterogen und uneinheitlich (kein „allgemeines lineares Modell“ für nicht-parametrischen Verfahren)
- Häufig wird Ranginformation der Daten verwendet
Tags: nicht-parametrische Verfahren, parametrische Verfahren
Quelle: VO09
Quelle: VO09
Was ist der unterschied zwischen parametrischen und nicht-parametrischen Verfahren hinsichtlich
- Effizienz
- Messniveau
- Voraussetzungen
- Effizienz
- Messniveau
- Voraussetzungen
Effizienz
Messniveau
Mathematisch-statistische Voraussetzungen
- Prüfung der Voraussetzungen für parametrische Tests jedoch häufig problematisch
- Erfolgt i. d. R. anhand der Stichprobe
- Voraussetzungen beziehen sich aber eigentlich auf Populationscharakteristika
- Bei Zutreffen ihrer Voraussetzungen haben parametrische Verfahren i. A. eine größere Effizienz - höhere Testmacht (p-Werte kleiner)
- Treffen Voraussetzungen nicht zu nicht-parametrische Methoden i. d. R. effizienter
Messniveau
- Metrisches Messniveau für parametrische Tests
- für alle anderen Skalenniveaus muss nicht-parametrisch getestet werden
Mathematisch-statistische Voraussetzungen
- Parametrische Verfahren stellen immer Voraussetzungen an die Verteilung der Daten
- Nicht-parametrische Verfahren benötigen ebenso öfter stetige Variablen und häufig auch die Homogenität der Populationsverteilungen
- Prüfung der Voraussetzungen für parametrische Tests jedoch häufig problematisch
- Erfolgt i. d. R. anhand der Stichprobe
- Voraussetzungen beziehen sich aber eigentlich auf Populationscharakteristika
Tags: nicht-parametrische Verfahren, parametrische Verfahren, Voraussetzungen
Quelle: VO09
Quelle: VO09
Welche Probleme gibt es bei Voraussetzungstest für parametrische Verfahren?
Prüfung der Voraussetzungen für parametrische Tests jedoch häufig problematisch: Erfolgt i. d. R. anhand der Stichprobe, Voraussetzungen beziehen sich aber eigentlich auf Populationscharakteristika
Probleme von Voraussetzungstests
Werden kleine Stichproben untersucht, können Voraussetzungen parametrischer Verfahren häufig nur ungenügend untersucht werden
Autoren wie Bortz und Lienert (2008, S. 59) plädieren deshalb dafür, bei kleineren Stichproben (N < 30) grundsätzlich nicht-parametrisch zu testen
Zentrales Grenzwerttheorem
Besagt, dass z.B. Mittelwerte sich ab etwa N = 30 normalverteilen, unabhängig von eigentlicher Verteilung der Messwerte - trägt zur Robustheit parametrischer Verfahren bei
Generell lässt sich folgern, dass, wenn nur kleine Stichproben (N < 30) untersucht werden können (vgl. Bortz & Lienert, 2008, S. 52)
Probleme von Voraussetzungstests
- beruhen meist ebenso auf parametrischen Voraussetzungen z.B. F-Test zur Überprüfung der Homogenität von Varianzen beruht auf der Annahme der Normalverteilung der Daten
- ' Stichprobengröße (vgl. Kapitel zu Effektgrößen) - kleines N - geringe Testmacht - Verletzungen werden u. U. nicht erkannt- großes N - hohe Testmacht - bereits unbedeutende Abweichungen werden auffällig
Werden kleine Stichproben untersucht, können Voraussetzungen parametrischer Verfahren häufig nur ungenügend untersucht werden
Autoren wie Bortz und Lienert (2008, S. 59) plädieren deshalb dafür, bei kleineren Stichproben (N < 30) grundsätzlich nicht-parametrisch zu testen
Zentrales Grenzwerttheorem
Besagt, dass z.B. Mittelwerte sich ab etwa N = 30 normalverteilen, unabhängig von eigentlicher Verteilung der Messwerte - trägt zur Robustheit parametrischer Verfahren bei
Generell lässt sich folgern, dass, wenn nur kleine Stichproben (N < 30) untersucht werden können (vgl. Bortz & Lienert, 2008, S. 52)
- Nicht-parametrisch getestet werden sollte
- Möglichst große Effekte untersucht werden sollten
- Signifikante Ergebnisse i. d. R. auch auf große Effekte schließen lassen - Replikation wichtig !
Tags: nicht-parametrische Verfahren, parametrische Verfahren, Voraussetzungen
Quelle: VO09
Quelle: VO09
Was besagt das zentrale Grenzwerttheorem?
Zentrales Grenzwerttheorem
Besagt, dass z.B. Mittelwerte sich ab etwa N = 30 normalverteilen, unabhängig von eigentlicher Verteilung der Messwerte - trägt zur Robustheit parametrischer Verfahren bei.
Bei größeren Stichproben (N > 30) sind insbesondere Verteilungsannahmen für parametrische Tests häufig vernachlässigbar.
Generell lässt sich folgern, dass, wenn nur kleine Stichproben (N < 30) untersucht werden können (vgl. Bortz & Lienert, 2008, S. 52)
Besagt, dass z.B. Mittelwerte sich ab etwa N = 30 normalverteilen, unabhängig von eigentlicher Verteilung der Messwerte - trägt zur Robustheit parametrischer Verfahren bei.
Bei größeren Stichproben (N > 30) sind insbesondere Verteilungsannahmen für parametrische Tests häufig vernachlässigbar.
Generell lässt sich folgern, dass, wenn nur kleine Stichproben (N < 30) untersucht werden können (vgl. Bortz & Lienert, 2008, S. 52)
- Nicht-parametrisch getestet werden sollte
- Möglichst große Effekte untersucht werden sollten
- Signifikante Ergebnisse i. d. R. auch auf große Effekte schließen lassen - Replikation wichtig !
Tags: nicht-parametrische Verfahren, parametrische Verfahren, Stichprobe
Quelle: VO09
Quelle: VO09
Was sind Nachteile nicht-parametrischer Verfahren?
Größerer Nachteil nicht-parametrischer Verfahren:
Nicht jeder parametrische Test hat eine nicht-parametrische Entsprechung
Multivariate (mehr als eine AV) und multifaktorielle Designs (mehr als eine UV) häufig nicht nicht-parametrisch testbar.
In der Praxis:
Weiterer Nachteil nicht-parametrischer Verfahren:
Jedoch weisen die meisten nicht-parametrischen Tests asymptotische Eigenschaften auf
Nicht jeder parametrische Test hat eine nicht-parametrische Entsprechung
Multivariate (mehr als eine AV) und multifaktorielle Designs (mehr als eine UV) häufig nicht nicht-parametrisch testbar.
In der Praxis:
- Transformation der Daten, damit Verteilungsannahmen eher zutreffen (Log-/Wurzel-/Power-Transformationen, Box-Cox-Transformationen)
- Verwendung parametrischer Methoden, die nicht Normalverteilung oder Varianzhomogenität benötigen (z.B. linear mixed models, generalized mixed models)
Weiterer Nachteil nicht-parametrischer Verfahren:
- Effektstärken undefiniert
- p-Werte müssen (bei händischer Berechnung) bei kleinem N aus Tabellen abgelesen werden, da sie auf Permutationen und nicht auf definierten Prüfverteilungen (z.B. t-Verteilung) beruhen
Jedoch weisen die meisten nicht-parametrischen Tests asymptotische Eigenschaften auf
- wenn N genügend groß, folgen Teststatistiken definierten Verteilungen z.B. Standardnormalverteilung, χ2-Verteilung
- Dadurch können Power- und Effektstärkenberechnungen approximativ durchgeführt werden (vgl. Bortz & Lienert, 2008, S. 48f.)
Tags: nicht-parametrische Verfahren, parametrische Verfahren
Quelle: VO09
Quelle: VO09
Was sind Beispiele (5) für nicht-parametrische Verfahren?
- Mediantest H0: Die beiden Stichproben stammen aus Populationen mit gleichem Median bzw.H0: Die k Stichproben stammen aus Populationen mit gleichem Median
- U-Test H0: Die beiden Stichproben stammen aus formgleich (homomer) verteilten Populationen mit gleichem Median
- Kruskal-Wallis-Test ist Verallgemeinerung der Prinzipien des U-Test für k > 2 Stichproben („klassisches“ Pendant der einfaktoriellen ANOVA)H0: Die k Stichproben stammen aus formgleich (homomer) verteilten Populationen mit gleichem Median
- Jonckheere-Terpstra-Test H1: Die Mediane der k Stichproben folgen einer schwach monotonen Rangordnung:
- McNemar-Test ist einfachstes nicht-parametrisches Verfahren zur Untersuchung dichotomer Merkmale in 2 abhängigen Stichproben (Test zweier abhängiger prozentualer Anteile)
 (an zumindest einer Stelle muss das „
(an zumindest einer Stelle muss das „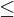 “ durch ein „
“ durch ein „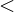 “ ersetzbar sein)
“ ersetzbar sein)Tags: nicht-parametrische Verfahren
Quelle: VO09, VO10
Quelle: VO09, VO10
Was prüft der Mediantest?
Nicht-parametrische Verfahren / 2 unabhängige Stichproben
Mediantest prüft 2 unabhängige Stichproben auf Unterschiede in ihrer zentralen Tendenz (ist – neben U-Test – eine nicht-parametrische Entsprechung zum t-Test für unabhängige Stichproben)
H0: Die beiden Stichproben stammen aus Populationen mit gleichem Median
Verwendet Ranginformation der Daten geeignet für (originär)
ordinalskalierte und metrische abhängige Variablen
Mediantest ist i. A. der schwächste nicht-parametrische Test zur Untersuchung von Lageunterschieden.
Allerdings: sehr robust gegenüber Ausreißern, macht keinerlei Annahmen zur Form oder Homogenität der Verteilung in den Stichproben
Mediantest prüft 2 unabhängige Stichproben auf Unterschiede in ihrer zentralen Tendenz (ist – neben U-Test – eine nicht-parametrische Entsprechung zum t-Test für unabhängige Stichproben)
H0: Die beiden Stichproben stammen aus Populationen mit gleichem Median
Verwendet Ranginformation der Daten geeignet für (originär)
ordinalskalierte und metrische abhängige Variablen
Mediantest ist i. A. der schwächste nicht-parametrische Test zur Untersuchung von Lageunterschieden.
Allerdings: sehr robust gegenüber Ausreißern, macht keinerlei Annahmen zur Form oder Homogenität der Verteilung in den Stichproben
Tags: Medientest, nicht-parametrische Verfahren
Quelle: VO09
Quelle: VO09
Wie wird der Mediantest durchgeführt?
Mediantest prüft 2 unabhängige Stichproben auf Unterschiede in ihrer zentralen Tendenz
Prinzip:


Gruppe A und B unterscheiden sich signifikant hinsichtlich ihrer zentralen Tendenz
Prinzip:
- Für beide Stichproben wird ein gemeinsamer Median bestimmt
- Auszählen, wie viele Messwerte in den jeweiligen Stichproben über und unter diesem Wert liegen
- Durchführen eines Vier-Felder-Tests (exakt oder asymptotisch)


Gruppe A und B unterscheiden sich signifikant hinsichtlich ihrer zentralen Tendenz
- Fällt bei ungeradzahligem N = N1 + N2 ein Messwert genau auf den gemeinsamen Median, kann dieser Messwert exkludiert werden
- Ansonsten kann auch ein Paramediantest durchgeführt werden - Dichotomisierung nahe am Median, um zu verhindern, dass Messwerte mit dem Trennwert identisch sind (vgl. Bortz & Lienert, 2008, S. 137)
- In SPSS wird eine Aufteilung in die Gruppen > Median und
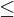 Median vorgenommen
Median vorgenommen
- Mediantest kann auch einseitig durchgeführt werden (beim Vergleich zweier Stichproben, df = 1) - Halbierung des p-Wertes
- Kann auch sehr einfach für den Vergleich von k > 2 Gruppen erweitert werden - keine Vier-Felder-Tafel, sondern k × 2 -Kontingenztafel
- Mediantest findet sich deshalb in SPSS unter Verfahren zum Vergleich von mehr als 2 Stichproben
Tags: Mediantest, nicht-parametrische Verfahren
Quelle: VO09
Quelle: VO09
Was zeigt dieser SPSS Ausdruck:


Mediantest prüft 2 unabhängige Stichproben auf Unterschiede in ihrer zentralen Tendenz


Tags: Mediantest, nicht-parametrische Verfahren, SPSS
Quelle: VO09
Quelle: VO09
Was prüft der U-Test?
Nicht-parametrische Verfahren / 2 unabhängige Stichproben
U-Test (Mann & Whitney, 1947; auch Wilcoxon-Rangsummentest [Wilcoxon, 1945] genannt) ist das nicht-parametrische Pendant zum t-Test für unabhängige Stichproben
U-Test (Mann & Whitney, 1947; auch Wilcoxon-Rangsummentest [Wilcoxon, 1945] genannt) ist das nicht-parametrische Pendant zum t-Test für unabhängige Stichproben
- Prüft zwei unabhängige Verteilungen auf Unterschiede hinsichtlich ihrer zentralen Tendenz
- H0: Die beiden Stichproben stammen aus formgleich (homomer) verteilten Populationen mit gleichem Median
- U-Test macht Annahme, dass die Form beider Verteilungen gleich ist (Unterschied zum Mediantest! Verteilungen müssen aber nicht symmetrisch oder gar normal sein)
- Verwendet Ranginformation der Daten geeignet für (originär) ordinalskalierte und metrische abhängige Variablen
Tags: nicht-parametrische Verfahren, U-Test
Quelle: VO09
Quelle: VO09
Was sind die Prinzipien des U-Test? Wie wird er berechnet?
Prinzip des U-Tests:
Rational: Wenn sich die Stichproben nicht in ihrer zentralen Tendenz (Median) unterscheiden, unterscheiden sie sich auch nicht in ihren mittleren Rängen



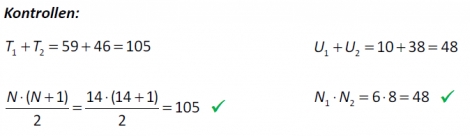
Unser Beispiel: U = 10, exakter Test, zweiseitig: p = .081 /einseitig: p = .041
- Die Messwerte beider Stichproben werden in eine gemeinsame Rangreihe gebracht (kleine Messwerte = niedrige Ränge)
- Rangsumme (U-Test) bzw. mittleren Rangplatz (Wilcoxon- Rangsummentest) pro Gruppe bestimmen
- Bestimmung der statistischen Größe U anhand der Rangsummen bzw. von W anhand der mittleren Ränge- inferenzstatistische Absicherung
Rational: Wenn sich die Stichproben nicht in ihrer zentralen Tendenz (Median) unterscheiden, unterscheiden sie sich auch nicht in ihren mittleren Rängen




- Exakter Test für N1 ≤ N2 ≤ 20 Tabellen in Lehrbüchern bei händischer Berechnung
- Asymptotischer Test für größere Stichproben

Unser Beispiel: U = 10, exakter Test, zweiseitig: p = .081 /einseitig: p = .041
Tags: nicht-parametrische Verfahren, U-Test
Quelle: VO09
Quelle: VO09
Was sind Vorteile des U-Tests gegenüber dem Mediantest? Wann sollte jedoch der Mediantest verwendet werden (4 Gründe)?
U-Test hat höhere Testmacht – wenn seine Voraussetzungen zutreffen – als Mediantest (nutzt mehr Information aus den Daten).
U-Test verliert an Macht und Gültigkeit, wenn (vgl. Bortz & Lienert, 2008)
... in diesen Fällen eher Mediantest verwenden
Das Vorliegen von Bindungen beeinträchtigt ebenso die Prüfgröße U - Bindungen sollten für Signifikanztestung berücksichtigt werden
U-Test verliert an Macht und Gültigkeit, wenn (vgl. Bortz & Lienert, 2008)
- Ausreißer vorliegen
- Stichproben ungleich groß sind
- Daten in kleinerer Stichprobe mehr streuen als in größerer
- Boden- oder Deckeneffekte vorliegen
... in diesen Fällen eher Mediantest verwenden
Das Vorliegen von Bindungen beeinträchtigt ebenso die Prüfgröße U - Bindungen sollten für Signifikanztestung berücksichtigt werden
Tags: Mediantest, nicht-parametrische Verfahren, U-Test
Quelle: VO09
Quelle: VO09
Wann spricht man von einer Bindung? Und wie muss dies bei einem U-Test berücksichtigt werden?
Das Vorliegen von Bindungen beeinträchtigt die Prüfgröße U - Bindungen sollten für Signifikanztestung berücksichtigt werden
Bindungen treten auf, wenn gleichgroße Messwerte vorliegen - Messwerte „teilen“ sich dann Rangplätze

Alle drei Messwerte haben gleichen Rang (da gleichgroß)
Die Plätze 7, 8 und 9 werden für sie vergeben

Bindungskorrektur verkleinert Varianzschätzung ( ) der Prüfgröße U - Korrektur führt eher zur Verwerfung der H0 (vgl. Bortz & Lienert, 2008, S. 146)
) der Prüfgröße U - Korrektur führt eher zur Verwerfung der H0 (vgl. Bortz & Lienert, 2008, S. 146)
Bindungen treten auf, wenn gleichgroße Messwerte vorliegen - Messwerte „teilen“ sich dann Rangplätze

Alle drei Messwerte haben gleichen Rang (da gleichgroß)
Die Plätze 7, 8 und 9 werden für sie vergeben

Bindungskorrektur verkleinert Varianzschätzung (
 ) der Prüfgröße U - Korrektur führt eher zur Verwerfung der H0 (vgl. Bortz & Lienert, 2008, S. 146)
) der Prüfgröße U - Korrektur führt eher zur Verwerfung der H0 (vgl. Bortz & Lienert, 2008, S. 146)Tags: Bindung, nicht-parametrische Verfahren, U-Test
Quelle: VO09
Quelle: VO09
Welche Möglichkeiten (3) gibt es zur Berechnung der Effektgröße für den U-Test?
Für U-Test existiert keine eigenständige Definition einer Effektgröße
Allerdings:
Allerdings:
- Berechnung und Angabe des sog. relativen Effekts mithilfe der mittleren Rangsummen (Mann & Whitney, 1947)
- Maßzahl der stochastischen Tendenz interpretierbar als Wahrscheinlichkeit, dass eine Person aus Gruppe 2 einen höherer Wert als eine Person aus Gruppe 1 hat
- Weitere Möglichkeit über asymptotische Eigenschaften von U: Verteilung von U kann mithilfe von z-Verteilung (Standardnormalverteilung) approximiert werden - approximative Bestimmung der Effektgröße r


Tags: Effektgröße, nicht-parametrische Verfahren, U-Test
Quelle: VO09
Quelle: VO09
Was zeigt dieser SPSS-Ausdruck bzw. die berechneten Werte:




Nicht-parametrische Verfahren: U-Test
Tabelle Ränge:
Angabe der mittleren Ränge und Rangsummen
Blick auf mittlere Ränge erlaubt Überprüfung, in welcher Gruppe niedrigere/höhere Werte vorlagen
Statistik für Test
Äquivalente Teststatistiken U und W, z- und p-Werte

Relativer Effekt interpretierbar als:
Die Wahrscheinlichkeit, dass eine Person aus Gruppe B einen höheren Wert als eine Person aus Gruppe A hat, beträgt (gerundet) nur 21%.
Approximatives Effektmaß deutet auf einen großen Effekt (| r | > .40) hin
Tabelle Ränge:
Angabe der mittleren Ränge und Rangsummen
Blick auf mittlere Ränge erlaubt Überprüfung, in welcher Gruppe niedrigere/höhere Werte vorlagen
Statistik für Test
Äquivalente Teststatistiken U und W, z- und p-Werte

Relativer Effekt interpretierbar als:
Die Wahrscheinlichkeit, dass eine Person aus Gruppe B einen höheren Wert als eine Person aus Gruppe A hat, beträgt (gerundet) nur 21%.
Approximatives Effektmaß deutet auf einen großen Effekt (| r | > .40) hin
Tags: nicht-parametrische Verfahren, SPSS, U-Test
Quelle: VO09
Quelle: VO09
Was prüft ein Medientest für k > 2 Stichproben?
Mediantest lässt sich auch für k > 2 Stichproben einsetzen
H0: Die k Stichproben stammen aus Populationen mit gleichem Median

H0: Die k Stichproben stammen aus Populationen mit gleichem Median
- Alternativhypothese hier nur ungerichtet möglich (Omnibustest, vgl. einfaktorielle ANOVA)
- Grundlage ist keine Vier-Felder-Tafel, sondern eine k × 2-Tafel

Tags: Mediantest, nicht-parametrische Verfahren
Quelle: VO09
Quelle: VO09
Was zeigt dieser SPSS-Ausdruck:




Nicht-parametrische Verfahren / k > 2 unabhängige Stichproben: Mediantest

Testergebnis:
Gemeinsamer Median = 10

Testergebnis:
Gemeinsamer Median = 10
- signifikanter Unterschied im Test über alle drei Gruppen; stärkere Wirkung von Präparaten A und B gegenüber C (aus Kontingenztafel gefolgert)
- ANOVA: p = .122 nicht signifikant
- Exakter Test notwendig, da in allen 6 Zellen die erwarteten Häufigkeiten < 5 sind!
Tags: Mediantest, nicht-parametrische Verfahren
Quelle: VO09
Quelle: VO09
Was prüft der Kruska-Wallis-Test? Wie wird dieser noch genannt?
Kruskal-Wallis-Test (H-Test; Kruskal & Wallis, 1952) ist Verallgemeinerung der Prinzipien des U-Test für k > 2 Stichproben
„klassisches“ Pendant der einfaktoriellen ANOVA
H0: Die k Stichproben stammen aus formgleich (homomer) verteilten Populationen mit gleichem Median
H-Test beruht ebenso auf Berechnung von Rangsummen und mittleren Rängen wie U-Test und Wilcoxon-Rangsummentest
Teststatistik H (bei größeren Stichproben) χ2-verteilt, mit df = k − 1

„klassisches“ Pendant der einfaktoriellen ANOVA
H0: Die k Stichproben stammen aus formgleich (homomer) verteilten Populationen mit gleichem Median
H-Test beruht ebenso auf Berechnung von Rangsummen und mittleren Rängen wie U-Test und Wilcoxon-Rangsummentest
Teststatistik H (bei größeren Stichproben) χ2-verteilt, mit df = k − 1

- Ebenso wie für U-Test gibt es eine Bindungskorrektur - vergrößert Wert der Teststatistik, führt eher zur Verwerfung der H0
- Alternativhypothese des H-Tests nur ungerichtet (Omnibustest)
- Bei kleinen Stichproben exakter Test, ansonsten asymptotischer Test - Asymptotischer Test hinreichend genau, wenn kleinste Stichprobe > 5
- Mediantest kann (ebenso wie im Fall k = 2) auch im Fall k > 2 mächtiger sein als H-Test; i. A. hat H-Test aber mehr Macht (mehr Information)
Tags: H-Test, Kruska-Wallis-Test, nicht-parametrische Verfahren
Quelle: VO10
Quelle: VO10
Wie lassen sich beim Kruska-Wallis-Test (H-Test) Effekte berechnen?
Analog zu U-Test lassen sich relative Effekte berechnen

Stochastische Tendenz, dass Personen der j-ten Gruppe höhere Werte als durchschnittlich alle anderen Gruppen erzielten
Welche Gruppen sich bei signifikantem Omnibustest signifikant
voneinander unterscheiden, kann im H-Test (analog zur ANOVA) mittels Kontrasten und Post-Hoc-Prozeduren untersucht werden.

Stochastische Tendenz, dass Personen der j-ten Gruppe höhere Werte als durchschnittlich alle anderen Gruppen erzielten
Welche Gruppen sich bei signifikantem Omnibustest signifikant
voneinander unterscheiden, kann im H-Test (analog zur ANOVA) mittels Kontrasten und Post-Hoc-Prozeduren untersucht werden.
Tags: H-Test, Kruska-Wallis-Test, nicht-parametrische Verfahren
Quelle: VO10
Quelle: VO10
Was zeigt der SPSS-Ausdruck zu diesem Beispiel:
In Untersuchung der BDI-Werte von Depressiven, Remittierten und Gesunden war in der Gruppe der Gesunden keine Normalverteilung gegeben.
Kann Ergebnis der ANOVA mit nicht-parametrischen Methoden bestätigt werden?


In Untersuchung der BDI-Werte von Depressiven, Remittierten und Gesunden war in der Gruppe der Gesunden keine Normalverteilung gegeben.
Kann Ergebnis der ANOVA mit nicht-parametrischen Methoden bestätigt werden?


Ränge:
Mittlere Ränge: niedrigste bei den Gesunden, höchste bei den Depressiven
Statistik für Test
Testergebnis signifikant - p < .001
Zum Vergleich:
Mediantest ebenso signifikant (p < .001), geringere Testmacht zeigt sich aber in niedrigerem χ2-Wert (χ2 = 58.65, df = 2)
Mittlere Ränge: niedrigste bei den Gesunden, höchste bei den Depressiven
Statistik für Test
Testergebnis signifikant - p < .001
Zum Vergleich:
Mediantest ebenso signifikant (p < .001), geringere Testmacht zeigt sich aber in niedrigerem χ2-Wert (χ2 = 58.65, df = 2)
Tags: H-Test, Kruska-Wallis-Test, nicht-parametrische Verfahren, SPSS
Quelle: VO10
Quelle: VO10
Wie kann man die relativen Effekte bei diesem Beispiel interpretieren?




Gesunde haben die niedrigste Wahrscheinlichkeit höhere Werte als alle anderen aufzuweisen, Depressive haben die höchste Wahrscheinlichkeit
Tags: Effektgröße, H-Test, Kruska-Wallis-Test, nicht-parametrische Verfahren
Quelle: VO10
Quelle: VO10
Was prüft der Jonckheere-Terpstra-Test? Welche Voraussetzung hat dieser?
Ähnlich wie in ANOVA kann auch nicht-parametrisch das Vorhandensein eines (monotonen) Trends untersucht werden - Jonckheere-Terpstra-Test
Test „funktioniert“ ähnlich wie H-Test (ist ebenso ein Omnibustest;
gleiche H0):
Test „funktioniert“ ähnlich wie H-Test (ist ebenso ein Omnibustest;
gleiche H0):
- H0: Die k Stichproben stammen aus formgleich (homomer) verteilten Populationen mit gleichem Median
- Allerdings wird auch eine Rangordnung in der unabhängigen Variable angenommen - Testrational entspricht einem additiven Verfahren einseitiger U-Tests
- H1: Die Mediane der k Stichproben folgen einer schwach monotonen Rangordnung:
 (an zumindest einer Stelle muss das „
(an zumindest einer Stelle muss das „
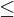 “ durch ein „
“ durch ein „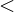 “ ersetzbar sein)
“ ersetzbar sein)- Anwendung des Jonckheere-Terpstra-Test setzt voraus, dass schon a priori Annahmen zur Rangreihung der unabhängigen Variable vorliegen (wie in ANOVA) - Prüfung dieser Annahme, keine a posteriori Bestätigung !
- Verfahren führt (asymptotisch, wenn N groß genug) zu einer z-verteilten Prüfstatistik
- Für Testung in SPSS muss die unabhängige Variable so kodiert sein, dass sie der zu testenden Rangreihung entspricht (analog in ANOVA)
Tags: Jonckheere-Terpstra-Test, nicht-parametrische Verfahren
Quelle: VO10
Quelle: VO10
Was zeigt dieser SPSS-Ausdruck:


nicht-parametrische Verfahren / k > 2 unabhängige Stichproben: Jonckheere-Terpstra-Test
- J-T-Statistiken dienen der Berechnung einer z-verteilten Prüfvariable („standardisierte J-TStatistik“)
- „Asymptotische Signifikanz“ basiert auf der Heranziehung der Standardnormalverteilung als Prüfverteilung - p < .001; die Mediane weisen eine monotone Ordnung auf(zur Erinnerung: Depressive = 31.50, Remittierte = 17,Gesunde = 7)
Tags: Jonckheere-Terpstra-Test, nicht-parametrische Verfahren, SPSS
Quelle: VO10
Quelle: VO10
Was prüft der McNemar-Test? Wann wird dieser angewendet?
Nicht-parametrische Verfahren / 2 abhängige Stichproben:
McNemar-Test (McNemar, 1947) ist einfachstes nicht-parametrisches Verfahren zur Untersuchung dichotomer Merkmale in 2 abhängigen Stichproben (Test zweier abhängiger prozentualer Anteile)
- Häufigkeitentest, χ2-Test (basiert auf einer 4-Felder-Tafel)
Anwendung des McNemar-Test richtet sich nach dem Vorliegen abhängiger Datenstrukturen:
McNemar-Test (McNemar, 1947) ist einfachstes nicht-parametrisches Verfahren zur Untersuchung dichotomer Merkmale in 2 abhängigen Stichproben (Test zweier abhängiger prozentualer Anteile)
- Häufigkeitentest, χ2-Test (basiert auf einer 4-Felder-Tafel)
Anwendung des McNemar-Test richtet sich nach dem Vorliegen abhängiger Datenstrukturen:
- Ein Merkmal wird mehrfach gemessen (Veränderungsmessung)
- Zwei Stichproben werden parallelisiert (matched samples) -Aussagen dazu, ob ein Merkmal in einer Stichprobe häufiger vorhanden ist, als in der anderen
- Vergleich der Zuwachsraten von zwei Merkmalen in einer Stichprobe: verändern sich zwei Merkmale mit unterschiedlicher Häufigkeit durch z.B. eine Behandlung?
Tags: McNemar-Test, nicht-parametrische Verfahren
Quelle: VO10
Quelle: VO10
Was ist das Prinzip des McNemar-Tests? Welche Voraussetzungen müssen erfüllt sein?
Nicht-parametrische Verfahren / 2 abhängige Stichproben
Prinzip (Veränderungshypothese):
Voraussetzungen (vgl. χ2-Tests in Kontingenztafeln)
Falls Voraussetzung des asymptotischen Tests nicht gegeben ist, kann Binomialtest (= exakter Test) verwendet werden (mit Parametern p = .5 und N = b + c)
Wie für 4-Felder-Test kann auch eine Kontinuitätskorrektur verwendet werden konservativere Testung.
Prinzip (Veränderungshypothese):
- Wenn sich nichts geändert hat, sollten sich in den Zellen b und c keine Unterschiede zeigen (Zellen a und d tragen keine Information !)
- Erwartungswerte dieser Zellen:

- Inferenzstatistische Untersuchung über Vergleich dieser Erwartungswerte mit den beobachteten Werten in Zellen b und c


Voraussetzungen (vgl. χ2-Tests in Kontingenztafeln)
- Untersuchungsobjekte müssen eindeutig in das 4-Felder-Schema eingeordnet werden können
- Die erwarteten Häufigkeiten der Felder b und c sind > 5 (asymptotischer Test!)
Falls Voraussetzung des asymptotischen Tests nicht gegeben ist, kann Binomialtest (= exakter Test) verwendet werden (mit Parametern p = .5 und N = b + c)
Wie für 4-Felder-Test kann auch eine Kontinuitätskorrektur verwendet werden konservativere Testung.
Tags: McNemar-Test, nicht-parametrische Verfahren
Quelle: VO10
Quelle: VO10
Interpretiere den untenstehenden SPSS-Ausdruck für folgendes Beispiel:
Beispiel: (vgl. Meyer et al., 2005)
Kardiovaskuläre Erkrankungen bei Patienten mit Schizophrenie oder schizoaffektiven Störungen ein wichtiger Morbiditäts- und Mortalitätsfaktor. Metabolisches Syndrom (Fettleibigkeit, Hypertonie, veränderte Blutfettwerte, Insulinresistenz) ist ein Risikofaktor für kardiovaskuläre Erkrankungen. Unterschiedliche antipsychotische Medikamente nehmen unterschiedlichen Einfluss auf das Körpergewicht und das metabolische Syndrom.
Bewirkt die Gabe eines bestimmten Antipsychotikums (Risperidon vs. Olanzapin) eine Verringerung der Auftrittshäufigkeit eines metabolischen Syndroms (= Met S) bei übergewichtigen Risikopatienten (BMI > 26)?

Beispiel: (vgl. Meyer et al., 2005)
Kardiovaskuläre Erkrankungen bei Patienten mit Schizophrenie oder schizoaffektiven Störungen ein wichtiger Morbiditäts- und Mortalitätsfaktor. Metabolisches Syndrom (Fettleibigkeit, Hypertonie, veränderte Blutfettwerte, Insulinresistenz) ist ein Risikofaktor für kardiovaskuläre Erkrankungen. Unterschiedliche antipsychotische Medikamente nehmen unterschiedlichen Einfluss auf das Körpergewicht und das metabolische Syndrom.
Bewirkt die Gabe eines bestimmten Antipsychotikums (Risperidon vs. Olanzapin) eine Verringerung der Auftrittshäufigkeit eines metabolischen Syndroms (= Met S) bei übergewichtigen Risikopatienten (BMI > 26)?

Kreuztabelle:
Kreuztabelle mit den absoluten Häufigkeiten
Tabelle Chi-Quadrat-Test:
Exakter Test (= Binomialtest) wird durchgeführt
p = .008 (2-seitig) p = .004 (1-seitig)
= signifikantes Ergebnis - Es zeigt sich eine eindeutige Verringerung der Auftrittshäufigkeit eines metabolischen Syndroms.
Voraussetzung für McNemar-Test: Die erwarteten Häufigkeiten der Felder b und c sind > 5 (asymptotischer Test!)
Falls Voraussetzung des asymptotischen Tests nicht gegeben ist, kann Binomialtest (= exakter Test) verwendet werden.
Kreuztabelle mit den absoluten Häufigkeiten
Tabelle Chi-Quadrat-Test:
Exakter Test (= Binomialtest) wird durchgeführt
p = .008 (2-seitig) p = .004 (1-seitig)
= signifikantes Ergebnis - Es zeigt sich eine eindeutige Verringerung der Auftrittshäufigkeit eines metabolischen Syndroms.
Voraussetzung für McNemar-Test: Die erwarteten Häufigkeiten der Felder b und c sind > 5 (asymptotischer Test!)
Falls Voraussetzung des asymptotischen Tests nicht gegeben ist, kann Binomialtest (= exakter Test) verwendet werden.
Tags: McNemar-Test, nicht-parametrische Verfahren, SPSS
Quelle: VO10
Quelle: VO10
Was ist der Vorzeichentest? (Kennzeichen, H0, Prinzip)
- Vorzeichentest einer der ältesten nicht-parametrischen Tests überhaupt
- Geeignet für (originär) ordinalskalierte oder metrische Daten
- H0: Der erste Wert eines Messwertpaares ist mit der gleichen Wahrscheinlichkeit (p = .5) größer oder kleiner als der zweite Messwert(Bezieht sich nicht wie die meisten anderen Tests auf Mediane sondern auf MITTELWERTE)
- Prinzip des Tests: - Bildung der Differenzen der Messwertepaare- Notieren, ob Differenz positiv (+) oder negativ (−) [oder Null (0)]- Durchführen eines Binomialtests anhand jener Zahl (n+ oder n−), die kleiner ist- Parameter des Binomialtests: p = .5, N = n+ + n−
- Vorzeichentest stellt praktisch fast gar keine Voraussetzungen an die Daten - Messgrößen als solche können prinzipiell in ihrer exakten Größe völlig unbekannt sein- Solange eindeutig festgestellt werden kann, ob eine Verbesserung (+), Verschlechterung (−) oder ein Gleichbleiben (0) vorliegt, kann der Test angewandt werden
Tags: nicht-parametrische Verfahren, Vorzeichentest
Quelle: VO11
Quelle: VO11
Welche Rolle spielen die Nulldifferenzen beim Vorzeichentest?
Problematisch kann es sein, wenn viele Nulldifferenzen vorliegen
- Ausschließen aus der Testung begünstigt tendenziell die Verwerfung der H0
- Alternativ kann die Hälfte der Nulldifferenzen ein positives, die andere Hälfte ein negatives Vorzeichen erhalten und in die Testung inkludiert werden
Tags: nicht-parametrische Verfahren, Nulldifferenzen, Vorzeichentest
Quelle: VO11
Quelle: VO11
Was zeigt dieser SPSS-Ausdruck:


(Nicht parametrische Verfahren / 2 abhängige Stichproben: Vorzeichentest )
Tabelle Häufigkeiten:
Tabelle Statistik für Tests:
Asymptotischer Test (N groß genug) wird durchgeführt
p < .001 (2-seitig) p < .001 (1-seitig)
Tabelle Häufigkeiten:
- 53 Patienten zeigten eine Verbesserung (T2 < T1 „Negative Differenzen“)
- 3 Patienten zeigten eine Verschlechterung (T2 > T1 „Positive Differenzen“)
- 0 Patienten blieben gleich („Bindungen“)
Tabelle Statistik für Tests:
Asymptotischer Test (N groß genug) wird durchgeführt
p < .001 (2-seitig) p < .001 (1-seitig)
Tags: abhängige Daten, nicht-parametrische Verfahren, SPss
Quelle: VO11
Quelle: VO11
Was ist der Wilcoxon-Test? Was ist das Prinzip des Tests?
(nicht parametrische Verfahren: 2 abhängige Stichproben)
Wilcoxon-Test (Wilcoxon, 1945; auch Vorzeichenrangtest genannt) das Pendant des t-Tests für abhängige Stichproben
Prinzip des Tests:
Beispiel:

Rangsummen:
T(+) = 49
T(−) = 17

Wilcoxon-Test (Wilcoxon, 1945; auch Vorzeichenrangtest genannt) das Pendant des t-Tests für abhängige Stichproben
- Geeignet nur für metrische Daten
- H0: Die beiden abhängigen Stichproben stammen aus Verteilungen mit gleichem Median
Prinzip des Tests:
- Bildung der Differenzen di der Messwertepaare
- Rangreihung der absoluten Differenzen
- Notieren, ob Differenz positiv (+) oder negativ (−) [oder Null (0)]
- Bestimmung der positiven und negativen Rangsummen (vgl. U-Test) - Inferenzstatistische Absicherung
Beispiel:

Rangsummen:
T(+) = 49
T(−) = 17

Tags: nicht-parametrische Verfahren, Wilcoxon-Test
Quelle: VO11
Quelle: VO11
Wann wird für den Wilcoxon-Test ein exakter Test bzw. wann ein asymptotischer Test durchgeführt?
Exakter Test für N ≤ 50 Tabellen in Lehrbüchern
Asymptotischer Test für größere Stichproben

Unser Beispiel:
T = 17, exakter Test,
zweiseitig: p = .175
einseitig: p = .087
Asymptotischer Test für größere Stichproben

Unser Beispiel:
T = 17, exakter Test,
zweiseitig: p = .175
einseitig: p = .087
Tags: nicht-parametrische Verfahren, Wilcoxon-Test
Quelle: VO11
Quelle: VO11
Welche Rolle spielen Bindungskorrektur und Nulldiffernzen im Wilcoxon-Test?
Was ist der Unterschied zum Vorzeichentest?
Was ist der Unterschied zum Vorzeichentest?
Wie für U-Test gibt es eine Bindungskorrektur (vgl. Bortz & Lienert, 2008, S. 196), wenn gleiche Differenzwerte vorliegen Anwendung der Korrektur führt eher zur Verwerfung der H0
Fälle mit Nulldifferenzen können ebenso wie beim Vorzeichentest
Fälle mit Nulldifferenzen können ebenso wie beim Vorzeichentest
- ausgeschlossen werden (begünstigt tendenziell Verwerfung der H0)
- oder erhalten generell den Rang (p + 1)/2 (p = Anzahl der Nulldifferenzen; vgl. Bortz & Lienert, 2008, S. 196)
- Wilcoxon-Test i. A. effizienter als Vorzeichentest (verwendet mehr Information aus den Daten)
- i. A. robust gegenüber Dispersionsunterschieden in den abhängigen Messungen (Unterschiede in Streuungen haben keine großen Auswirkungen.)
- Allerdings: ─ Hohes Messniveau Voraussetzung des Tests─ Differenzen der Messungen müssen auf einer Intervallskala liegen - metrisches Messniveau erforderlich─ Unterschiede in der Dispersion können u. U. auch Testmachtschmälern - Vorzeichentest kann dann effizienter sein !
- Asymptotische Eigenschaften des Tests können zur Bestimmung einer approximativen Effektgröße wie im U-Test verwendet werden Verwendung des z-Wertes unter Heranziehung der Formel beim U-Test
Tags: nicht-parametrische Verfahren, Wilcoxon-Test
Quelle: VO11
Quelle: VO11
Was misst der Friedman-Test?
(Nicht-parametrische Verfahren / k > 2 abhängige Stichproben)
Friedman-Test (Friedman, 1937; auch Rangvarianzanalyse genannt) das nichtparametrische Pendant zur einfaktoriellen abhängigen ANOVA
Beispiel:

Wenn sich die abhängigen Messungen nicht in ihren Rangsummen unterscheiden, unterscheiden sie sich auch nicht in ihrer zentralen Tendenz (Median).
Friedman-Test (Friedman, 1937; auch Rangvarianzanalyse genannt) das nichtparametrische Pendant zur einfaktoriellen abhängigen ANOVA
- H0: Die k abhängigen Stichproben stammen aus Verteilungen mit gleichem Median
- Geeignet für (originär) ordinalskalierte und metrische Daten
- Prinzip des Tests: - Rangreihung der Messungen innerhalb jeder Beobachtungseinheit- Bestimmung der Rangsummen (vgl. U-Test) je Messung - Inferenzstatistische Absicherung
Beispiel:

Wenn sich die abhängigen Messungen nicht in ihren Rangsummen unterscheiden, unterscheiden sie sich auch nicht in ihrer zentralen Tendenz (Median).
- Teststatistik asymptotisch χ2-verteilt, mit df = k − 1 (vgl. Kruskal-Wallis-Test)
- Beispiel führt zu χ2 = 2.57, df = 2, p = .276 (asympt.), p = .305 (exakt) (2,57 – ist nicht signifikant – vielleicht ist die Stichprobe zu klein bzw. die Unterschiede zu klein.)
- Bindungskorrektur möglich (vgl. Bortz & Lienert, 2008, S. 205) - führt eher zur Verwerfung der H0
- Alternativhypothese des Friedman-Tests nur ungerichtet (Omnibustest)
- Bei kleinen Stichproben exakter Test

Tags: Friedman-Test, nicht-parametrische Verfahren
Quelle: VO11
Quelle: VO11
Wie können Kontraste und Post-Hoc-Tests für den Friedman-Test angewendet werden?
Kontraste
Post-Hoc-Tests
Beispiel: (vgl. Wilkinson-Tough et al., 2009)
Fallserie zur Untersuchung der Wirkung einer Mindfulness-basierten Therapiemethode bei Patienten mit Zwangsgedanken 7 Patienten, die im Rahmen eines A-B-C-Designs zunächst eine Phase ohne Behandlung (Phase A; 2 Wochen; Baseline), dann eine Phase in der sie angeleitet und selbständig Progressive Muskelrelaxation anwandten (Phase B; 2-3 Wochen; PMR) und eine Phase in der sie schließlich 6 wöchentliche einstündige Therapieeinheiten mit Psychoedukation und Mindfulness-basierter Psychotherapie erhielten (Phase C; 6 Wochen; Mindfulness). Die Patienten wurden aufgefordert, die in den Therapiephasen gelernten Übungen selbständig weiterzuführen. Zwei Monate nach Ende von Phase C wurde eine Katamnese durchgeführt.
Primäres Outcomemaß: YBOCS (Yale-Brown Obsessive-Compulsive Scale; Werte > 15 klinisch relevant)


- Wie im Fall des Kruskal-Wallis-Test Berechnung kritischer Differenzen der mittleren Rangsummen
- Durch Verwendung des kritischen Wertes wird eine implizite Fehlerkontrolle angewandt familywise error bleibt auf gewähltemα-Niveau

Post-Hoc-Tests
- Kritische Differenzen mit expliziter Fehlerkontrolle
- zα* ist kritischer z-Wert von α* (= Bonferroni-korrigiertes α) kann aus Tabellen abgelesen werden
- Vorgehen ist laut Field (2009) (im Wesentlichen) äquivalent zur Anwendung sequentieller Wilcoxon-Tests - stimmt nur bedingt, Voraussetzungen des Friedman- und des Wilcoxon-Tests sind nicht ident !

Beispiel: (vgl. Wilkinson-Tough et al., 2009)
Fallserie zur Untersuchung der Wirkung einer Mindfulness-basierten Therapiemethode bei Patienten mit Zwangsgedanken 7 Patienten, die im Rahmen eines A-B-C-Designs zunächst eine Phase ohne Behandlung (Phase A; 2 Wochen; Baseline), dann eine Phase in der sie angeleitet und selbständig Progressive Muskelrelaxation anwandten (Phase B; 2-3 Wochen; PMR) und eine Phase in der sie schließlich 6 wöchentliche einstündige Therapieeinheiten mit Psychoedukation und Mindfulness-basierter Psychotherapie erhielten (Phase C; 6 Wochen; Mindfulness). Die Patienten wurden aufgefordert, die in den Therapiephasen gelernten Übungen selbständig weiterzuführen. Zwei Monate nach Ende von Phase C wurde eine Katamnese durchgeführt.
Primäres Outcomemaß: YBOCS (Yale-Brown Obsessive-Compulsive Scale; Werte > 15 klinisch relevant)

- Kontraste: eine kritische Differenz für alle Einzelvergleiche kritischer χ2-Wert (α = .05, df = 3): 7.81
- Post-Hoc-Tests: Wilcoxon-Tests, α* = .05/3 = .017
- Effektstärken: anhand der z-Werte der Wilcoxon-Tests (sehr approximativ!!!)

Tags: Friedman-Test, Kontrast, nicht-parametrische Verfahren, Post-Hoc-Test
Quelle: VO11
Quelle: VO11
Was zeigt dieser SPSS-Ausdruck:


Ausgabe mittlerer Ränge (oben)
Nach der Mindfulness-Intervention sind die Werte am niedrigsten;
die höchstenWerte liegen zu Beginn vor (Baseline)
Tabelle Statistik für Test
Die H0 wird verworfen, p < .001 (asymptotischer Test)
Nach der Mindfulness-Intervention sind die Werte am niedrigsten;
die höchstenWerte liegen zu Beginn vor (Baseline)
Tabelle Statistik für Test
Die H0 wird verworfen, p < .001 (asymptotischer Test)
Tags: Friedman-Test, nicht-parametrische Verfahren, SPSS
Quelle: VO11
Quelle: VO11
Tags: nicht-parametrische Verfahren, SPSS, Wilcoxon-Test
Quelle: VO11
Quelle: VO11
Kartensatzinfo:
Autor: coster
Oberthema: Psychologie
Thema: Statistik
Schule / Uni: Universität Wien
Ort: Wien
Veröffentlicht: 21.06.2013
Schlagwörter Karten:
Alle Karten (175)
4-Felder-Tafel (17)
abhängige Daten (6)
ALM (1)
ANCOVA (3)
ANOVA (15)
Bindung (1)
Cohens d (10)
Cohens Kappa (6)
Effektgröße (31)
Einzelvergleich (2)
Einzelvergleiche (1)
Eta (7)
Fehler (1)
Friedman-Test (3)
H-Test (5)
Haupteffekt (2)
Haupteffekte (1)
Interaktion (5)
Konkordanz (4)
Kontrast (11)
Kontrollvariable (1)
MANOVA (2)
McNemar-Test (4)
Mediantest (5)
Medientest (1)
mixed ANOVA (10)
nicht-parametrische Verfahren (36)
NNT (3)
Normalverteilung (3)
NPV (4)
Nulldifferenzen (1)
odds ratio (7)
partielle Eta (5)
phi-Koeffizient (1)
Phi-Koeffizienz (1)
Planung (1)
Post-Hoc-Test (4)
Post-hoc-Tests (3)
Power (1)
PPV (4)
Prävalenz (6)
r (4)
Reliabilität (1)
risk ratio (7)
Sensitivität (6)
Signifikanz (6)
Spezifität (6)
Sphärizität (2)
SPSS (14)
SPss (1)
Stichprobe (3)
Störvariable (1)
t-Test (7)
Testmacht (2)
Trends (1)
U-Test (6)
Varianz (2)
Varianzanalyse (11)
Varianzschätzer (1)
Voraussetzungen (2)
Vorzeichentest (2)
Wechselwirkung (3)
Wilcoxon-Test (4)
x2-Test (5)






