Was sind die Beispiele für varianzanalytische Methoden?
– Einfaktorielle Versuchspläne
– Einzelvergleiche (Kontraste) und Post-Hoc-Tests
– Zweifaktorielle Versuchspläne – Haupteffekte & Wechselwirkungen
– Simultaner Vergleich von 2 Gruppen zu 2 Zeitpunkten (klassisches Design der Interventionsforschung) – abhängige Messungen
– (Ausblick auf) Kovarianzanalyse
– Einzelvergleiche (Kontraste) und Post-Hoc-Tests
– Zweifaktorielle Versuchspläne – Haupteffekte & Wechselwirkungen
– Simultaner Vergleich von 2 Gruppen zu 2 Zeitpunkten (klassisches Design der Interventionsforschung) – abhängige Messungen
– (Ausblick auf) Kovarianzanalyse
Tags: Varianzanalyse
Source: VO01
Source: VO01
Was versteht man unter der einfaktoriellen Varianzanalyse? Nenne ein Beispiel und die Vorteile der Durchführung einer einfaktoriellen Varianzanalyse.
- Einfaktorielle Varianzanalyse (ANOVA) erlaubt simultanen Vergleich von k ≥ 2 Mittelwerten
- „Erweiterung“ des t-Test für k > 2 Gruppen

Warum keine drei t-Tests (Depressive vs. Remittierte; Depressive vs. Gesunde; Remittierte vs. Gesunde) ?
Problem der Alphafehler-Kumulierung Jeder statistische Test hat (selbstgewählte) Irrtumswahrscheinlichkeit Alphafehler/Fehler 1. Art (meistens: α = 0.05)
Der gemeinsame Fehler (familywise error) ist fast dreimal höher als der nominell gewählte. Die Zuwachsrate steigt mit Anzahl der Gruppen und Vergleiche stark an.
Für den simultanen Vergleich mehrerer Gruppenmittelwerte ist ANOVA somit das geeignete Analyseinstrument
– Kontrolliert den familywise error
– Ist aber nicht so konservativ wie alternative Prozeduren
Tags: ANOVA, Varianzanalyse
Source: VO01
Source: VO01
Warum ist beim simultanen Vergleich mehrerer Gruppenmittelwerte die ANOVA sinnvoll und nicht der Einsatz mehrerer t-Tests?

Warum keine drei t-Tests (Depressive vs. Remittierte; Depressive vs. Gesunde; Remittierte vs. Gesunde) ?

Problem der Alphafehler-Kumulierung
Jeder statistische Test hat (selbstgewählte) Irrtumswahrscheinlichkeit: Alphafehler/Fehler 1. Art (meistens: α = 0.05)
Wenn die
 in Wirklichkeit gilt, wird sie (dennoch) in (nur) 5 von 100 Fällen verworfen (bei α = 0.05)
in Wirklichkeit gilt, wird sie (dennoch) in (nur) 5 von 100 Fällen verworfen (bei α = 0.05)Der Alphafehler von drei t-Tests zusammen ist somit sicherlich größer als jener bloß eines (t-)Tests - Nur:Wie groß ?
Annahme: Ergebnisse der t-Tests voneinander statistisch unabhängig
Wahrscheinlichkeit für einen Alphafehler bei einem Test ist gleich α

Statistische Unabhängigkeit - Multiplikationstheorem
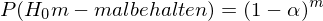
Gegenwahrscheinlichkeit: in m Tests mindestens einmal die
 (fälschlicherweise) verwerfen
(fälschlicherweise) verwerfen
α = 0.05, k = 3 Gruppen, m = 3 t-Tests

Der gemeinsame Fehler (familywise error) ist fast dreimal höher als der nominell gewählte.
Zuwachsrate steigt mit Anzahl der Gruppen und Vergleiche stark an:

Zudem: nicht alle Tests voneinander unabhängig reales Alpha höher!
Zur Kontrolle des familywise error können Prozeduren wie Bonferroni-Korrektur o. ä. verwendet werden - JEDOCH sehr konservatives Verfahren.
Für den simultanen Vergleich mehrerer Gruppenmittelwerte ist ANOVA somit das geeignete Analyseinstrument
– Kontrolliert den familywise error
– Ist aber nicht so konservativ wie alternative Prozeduren
Tags: ANOVA, t-Test, Varianzanalyse
Source: VO01
Source: VO01
Was versteht man unter einem familywise error?
Darunter versteht man den Fehler der akkumuliert wird wenn ein Test mehrfach auf eine Hypothese angewendet wird.
Warum keine drei t-Tests (Depressive vs. Remittierte; Depressive vs. Gesunde; Remittierte vs. Gesunde) ?
Problem der Alphafehler-Kumulierung
Jeder statistische Test hat (selbstgewählte) Irrtumswahrscheinlichkeit - Alphafehler/Fehler 1. Art (meistens: α = 0.05)
Beispiel:
α = 0.05, k = 3 Gruppen, m = 3 t-Tests

Der gemeinsame Fehler (familywise error) ist fast dreimal höher als der nominell gewählte.
Zur Kontrolle des familywise error können Prozeduren wie Bonferroni-Korrektur o. ä. verwendet werden.
Warum keine drei t-Tests (Depressive vs. Remittierte; Depressive vs. Gesunde; Remittierte vs. Gesunde) ?
Problem der Alphafehler-Kumulierung
Jeder statistische Test hat (selbstgewählte) Irrtumswahrscheinlichkeit - Alphafehler/Fehler 1. Art (meistens: α = 0.05)
Beispiel:
α = 0.05, k = 3 Gruppen, m = 3 t-Tests

Der gemeinsame Fehler (familywise error) ist fast dreimal höher als der nominell gewählte.
Zur Kontrolle des familywise error können Prozeduren wie Bonferroni-Korrektur o. ä. verwendet werden.
Tags: ANOVA, Fehler, t-Test, Varianzanalyse
Source: VO01
Source: VO01
Was ist die Bonferroni-Korrektur?
Zur Kontrolle des familywise error können Prozeduren wie Bonferroni-Korrektur o. ä. verwendet werden.

Nachteil: Sehr konservatives Vorgehen! (Verwerfen der H0 wird u. U. unverhältnismäßig schwierig; k = 3, α = 0.05: α* = 0.017)
Für den simultanen Vergleich mehrerer Gruppenmittelwerte ist ANOVA somit das geeignete Analyseinstrument
– Kontrolliert den familywise error
– Ist aber nicht so konservativ wie alternative Prozeduren

Nachteil: Sehr konservatives Vorgehen! (Verwerfen der H0 wird u. U. unverhältnismäßig schwierig; k = 3, α = 0.05: α* = 0.017)
Für den simultanen Vergleich mehrerer Gruppenmittelwerte ist ANOVA somit das geeignete Analyseinstrument
– Kontrolliert den familywise error
– Ist aber nicht so konservativ wie alternative Prozeduren
Tags: ANOVA, t-Test, Varianzanalyse
Source: VO01
Source: VO01
Was ist das Prinzip der Varianzanalyse?
Omnibustest
ANOVA prüft nicht sequentiell die Hypothesen
H0(1): μ1 = μ2 ; H0(2): μ1 = μ3 ; H0(3): μ2 = μ3 sondern
H0: μ1= μ2 = μ3 bzw. allgemein H0: μ1 = μ2 = … = μk
Die H1 wird angenommen, wenn sich zumindest zwei der untersuchten Mittelwerte signifikant voneinander unterscheiden

Test beruht auf einem Vergleich der Varianz der Daten, die durch
systematische Unterschiede bedingt wird (Gruppen), gegenüber der Varianz, die durch den Zufall zustande kommt → „Varianzanalyse“
Ist die Varianz der Gruppenmittelwerte um einen gemeinsamen Mittelwert größer als die Varianz innerhalb der Gruppen?
Beispiel: Depressive (rot) / Remittierte (blau) / Gesunde (grün)
Gruppenmittelwerte um einen gemeinsamen Mittelwert:

Varianz innerhalb der Gruppe:

ANOVA prüft nicht sequentiell die Hypothesen
H0(1): μ1 = μ2 ; H0(2): μ1 = μ3 ; H0(3): μ2 = μ3 sondern
H0: μ1= μ2 = μ3 bzw. allgemein H0: μ1 = μ2 = … = μk
Die H1 wird angenommen, wenn sich zumindest zwei der untersuchten Mittelwerte signifikant voneinander unterscheiden

Test beruht auf einem Vergleich der Varianz der Daten, die durch
systematische Unterschiede bedingt wird (Gruppen), gegenüber der Varianz, die durch den Zufall zustande kommt → „Varianzanalyse“
Ist die Varianz der Gruppenmittelwerte um einen gemeinsamen Mittelwert größer als die Varianz innerhalb der Gruppen?
Beispiel: Depressive (rot) / Remittierte (blau) / Gesunde (grün)
Gruppenmittelwerte um einen gemeinsamen Mittelwert:

Varianz innerhalb der Gruppe:

Tags: ANOVA, Varianzanalyse
Source: VO01
Source: VO01
Tags: ANOVA, Varianz, Varianzschätzer
Source: VO01
Source: VO01
Tags: ANOVA, Signifikanz, Varianzanalyse
Source: VO01
Source: VO01
Was zeigt dieser SPSS Auszug:





Interpretation: die Gruppen unterscheiden sich signifikant voneinander
- H0 wird verworfen
- Welche Gruppen zeigen signifikante Unterschiede?
Einzelvergleiche (Kontraste) und Post-Hoc-Tests
Tags: ANOVA, SPSS, Varianzanalyse
Source: VO01
Source: VO01
Welche Methoden können bei der Varianzanalyse verwendet werden um festzustellen zwischen welchen Gruppen es signifikante Unterschiede gibt?
- Einzelvergleiche (Kontraste)
- Post-Hoc-Tests
Einzelvergleiche häufig a priori formuliert, d.h. bereits vor Durchführung der Analyse besteht eine Hypothese, welche Mittelwerte sich voneinander unterscheiden sollten (hypothesengeleitetes Vorgehen)
Einzelvergleiche können aber auch a posteriori berechnet werden, ebenso wie Post-Hoc-Tests zur Datenexploration benutzt werden können (exploratives Vorgehen)
Tags: Einzelvergleiche, Post-Hoc-Test, Varianzanalyse
Source: VO01
Source: VO01
Was sind Einzelvergleiche bei der Varianzanalyse und wie werden diese durchgeführt?
Einzelvergleiche = Kontraste
Erlauben spezifische Gruppenvergleiche und auch gerichtete Hypothesen z.B.: Gesunde und Remittierte haben niedrigere Werte im BDI-II als akut Depressive
Rechnerische Durchführung durch Festlegung von Linearkombinationen bzw. gewichteter Summen der Gruppenmittelwerte

Zwei Kontraste sind orthogonal, wenn die Summe der Produkte ihrer Koeffizienten Null ist:

Beispiel SPSS:

(Die Kontrast-Koeffizienten sind die Gewichtung. Wenn zwei Gruppen den gleichen Kontrast-Koeffizienten haben, dann werden diese zusammengelegt und gegen die andere verglichen.
Kontrast 2: Depressive sind nicht relevant – deshalb haben sie das Gewicht 0
Ergebnis der Kontrasttests ist
Kontraste können für sequentielle Vergleiche von Gruppenmittelwerten verwendet werden.
Einseitige oder zweiseitige Testung in Kontrasten richtet sich nach dem Vorhandensein gerichteter Hypothesen
Erlauben spezifische Gruppenvergleiche und auch gerichtete Hypothesen z.B.: Gesunde und Remittierte haben niedrigere Werte im BDI-II als akut Depressive
Rechnerische Durchführung durch Festlegung von Linearkombinationen bzw. gewichteter Summen der Gruppenmittelwerte

- Orthogonale (= unabhängige) und nicht-orthogonale Kontraste möglich
- Allgemein:

Zwei Kontraste sind orthogonal, wenn die Summe der Produkte ihrer Koeffizienten Null ist:

Beispiel SPSS:

(Die Kontrast-Koeffizienten sind die Gewichtung. Wenn zwei Gruppen den gleichen Kontrast-Koeffizienten haben, dann werden diese zusammengelegt und gegen die andere verglichen.
Kontrast 2: Depressive sind nicht relevant – deshalb haben sie das Gewicht 0
Ergebnis der Kontrasttests ist
- Gesunde und Remittierte unterscheiden sich signifikant von Depressiven; einseitige Testung → p-Wert kann noch halbiert werden (t-Verteilung!)
- Gesunde unterscheiden sich auch signifikant von Remittierten; keine a priori Hypothese → Beibehalten des 2-seitigen p-Wertes aus SPSS
Kontraste können für sequentielle Vergleiche von Gruppenmittelwerten verwendet werden.
- Ausschluss jeweils einer Gruppe in nachfolgenden Kontrasttests (Kontrastkoeffizient = 0)
- stellt sicher, dass alle Kontraste orthogonal (= unabhängig) sind
Einseitige oder zweiseitige Testung in Kontrasten richtet sich nach dem Vorhandensein gerichteter Hypothesen
Tags: Einzelvergleich, Varianzanalyse
Source: VO01
Source: VO01
Was sieht man bei diesem SPSS Auszug? Interpretation?

ONEWAY ANOVA (ganz oben)
man sieht die Varianzanalyse - die Mittelwertsunterschiede sind hochsignifikant.
Die Kontrast-Koeffizienten sind die Gewichtung. Wenn zwei Gruppen den gleichen Kontrast-Koeffizienten haben, dann werden diese zusammengelegt und gegen die andere verglichen.
Kontrast 2: Depressive sind nicht relevant – deshalb haben sie das Gewicht 0
1. Kontrast: frei wählbar (mit allen Gruppen)
2. Kontrast: eine Gruppe muss rausfallen, damit man ein orthogonales Ergebnis erhält.
Der Kontrast wird formal mit der t-Verteilung geprüft.
Ergebnis der Kontrasttests ist
- t-Verteilung: 13,56 bei 104 Freiheitsgrade (hoch signifikant): Gesunde und Remittierte unterscheiden sich signifikant von Depressiven; einseitige Testung → p-Wert kann noch halbiert werden (t-Verteilung!)
- t-Verteilung: -4,07 bei 104 Freiheitsgraden (hoch signifikant): Gesunde unterscheiden sich auch signifikant von Remittierten; keine a priori Hypothese → Beibehalten des 2-seitigen p-Wertes aus SPSS
(Doppelte Ergebnisdarstellung:
Varianzen sind gleich und Varianzen sind nicht gleich... also es wird berechnet unter der Annahme, dass die Varianzen gleich sind
Voraussetzung für Varianzanalyse
- Varianzen innerhalb der einzelnen Gruppen müssen homogen sein.
- Wenn die Varianzen nicht gleich sind, rechnet SPSS tlw. eine Korrektur indem sie die Freiheitsgrade reduziert (dF) (Siehe Folie Einfaktorielle Versuchspläne 20)
Normalerweise betrachtet man den 1. Bereich (Varianzen gleich).
Tags: Einzelvergleich, Kontrast
Source: VO01
Source: VO01
Was bedeutet das Kontraste orthogonal oder nicht orthogonal sein können?
Kontraste können orthogonal oder nicht-orthogonal sein: Kontraste die orthogonal sind, bezeichnet das es Tests sind die statistisch unabhängig sind.
Zwei Kontraste sind orthogonal, wenn die Summe der Produkte ihrer Koeffizienten Null ist:
(es können numerisch beliebige Werte gewählt werden, solange sie null ergeben)

Abhängig davon wieviele Gruppen man definiert hat, kann eine bestimmte Anzahl an orthogonalen Kontrasten definiert werden (k-1 orthogonale Kontraste) (k=Anzahl der Gruppen)
Beispiel: 3 Gruppen = 2 orthogonale Kontraste (man kann auch andere Kontraste formulieren, diese sind aber dann nicht orthogonal)
Zwei Kontraste sind orthogonal, wenn die Summe der Produkte ihrer Koeffizienten Null ist:
(es können numerisch beliebige Werte gewählt werden, solange sie null ergeben)

Abhängig davon wieviele Gruppen man definiert hat, kann eine bestimmte Anzahl an orthogonalen Kontrasten definiert werden (k-1 orthogonale Kontraste) (k=Anzahl der Gruppen)
Beispiel: 3 Gruppen = 2 orthogonale Kontraste (man kann auch andere Kontraste formulieren, diese sind aber dann nicht orthogonal)
Tags: Kontrast, Polynomiale Kontraste
Source: VO02
Source: VO02
Welche Arten von Kontraste bietet SPSS zur Beobachtung von Trends an?

Trends: Reihung/Anordnung von Gruppen = Polynomiale Kontraste
linear: mind 2. Gruppen um dies eindeutig festlegen zu können
quadratisch (mind 3 Gruppen): 1 Gruppe hohe, 2. Gruppe niedrige, 3. Gruppe hohe Werte
kubisch (mind. 4 Gruppen notwendig)
Tags: Polynomiale Kontraste, Trends
Source: VO02
Source: VO02
Was sind polynomiale Kontraste? Wann kann dies sinnvoll berechnet werden?
Polynomiale Kontraste: Trends/Reihung/ordinaler Funktion von Gruppen (linear, quadratisch, kubisch)
Polynomiale Kontraste sind zueinander alle orthogonal.
Nur nützlich, wenn Gruppen sinnvolle und nicht beliebige Ordnung aufweisen (a-priori Ordnung muss bekannt sein).
Außerdem setzen polynomiale Kontraste das Prinzip Äquidistanz der Faktorstufen voraus (Gruppierungsvariable müsste ebenso intervallskaliert sein).
(dh. Die Depressiven sind von den Remittierten gleich weit entfernt sind wie die Gesunden von den Remittierten)
Polynomiale Kontraste können auch durch eigene Gewichtsetzung berechnet werden (Beispiel für linearen und quadratischen Kontrast).

Polynomiale Kontraste sind zueinander alle orthogonal.
Nur nützlich, wenn Gruppen sinnvolle und nicht beliebige Ordnung aufweisen (a-priori Ordnung muss bekannt sein).
Außerdem setzen polynomiale Kontraste das Prinzip Äquidistanz der Faktorstufen voraus (Gruppierungsvariable müsste ebenso intervallskaliert sein).
(dh. Die Depressiven sind von den Remittierten gleich weit entfernt sind wie die Gesunden von den Remittierten)
Polynomiale Kontraste können auch durch eigene Gewichtsetzung berechnet werden (Beispiel für linearen und quadratischen Kontrast).

Tags: Polynomiale Kontraste
Source: VO02
Source: VO02
Was zeigt dieser SPSS-Ausdruck/Graph?





Bei einem Freiheitsgrad (df=1) korrelieren F- und t-Test miteinander.
Polynomiale Kontraste werden immer zweiseitig getestet! (Bei dieser Testung ist also keine "Seitigkeit" verbunden)
Lineare Trend: es gibt eine ansteigende/absteigender Trend vor.
Auch in der grafischen Darstellung ist ein absteigender Trend sichtbar - dieser scheint linear zu sein, könnte ev. aber auch quadratisch sein.
Jetzt wurde noch eine weitere Auswertung durchgeführt (quadratisch):

Gruppenmittelwerte weisen nicht nur linearen Trend auf (p < .001), sondern auch quadratischen (p = .001)
Inhaltlich bedeutet dies hier, dass die Gruppenmittelwerte der Gesunden und Remittierten offenbar näher beieinander liegen, als jene der Remittierten und Depressiven (d.h. es existiert anscheinend keine Äquidistanz)
Tags: Polynomiale Kontraste
Source: VO02
Source: VO02
Welche unterschiedlichen Berechnungsmöglichkeiten für Kontraste/Einzelvergleiche können in SPSS gewählt werden? Was kennzeichnet diese?
Weitere (wählbare) Kontraste in der SPSS Prozedur ‚Allgemeines Lineares Modell‘.
Neben den polynomialen Kontrasten oder den selber wählbaren Kontrasten gibt es folgende:

(3 Kontraste sind nicht orthogonal)
Neben den polynomialen Kontrasten oder den selber wählbaren Kontrasten gibt es folgende:

(3 Kontraste sind nicht orthogonal)
- Einfacher Kontrast häufig verwendet eine Referenzgruppe wird mit allen anderen Gruppen verglichen Anmerkung: die Referenzgruppe die getestet werden möchte muss in SPSS zu Beginn oder am Ende kodiert sein.Es wird immer die gleiche Referenzgruppe genommen die mit den anderen Gruppen jeweils verglichen wird.Ist vor allem bei Versuchs-Kontrollgruppen-Designs.
- Differenz und Helmert im Prinzip gleiche Prozedur – einmal „von oben nach unten“ (Differenz), das andere Mal von „unten nach oben“ (Helmert) Differenz: Jeder Mittelwert der Gruppe wird mit dem Mittelwert der vorhergehenden Gruppe verglichen
- Wiederholt eignet sich, um sequenziell alle paarweisen Mittelwertsunterschiede zu testen Gruppe1 mit Gruppe 2, Gruppe 2 und Gruppe 3, Gruppe 3 mit Gruppe 4
Tags: Kontrast, Polynomiale Kontraste, SPSS
Source: VO02
Source: VO02
Was zeigt dieser SPSS Ausdruck?

(Gruppe 1: Depressive, Gruppe 2: Remittierte, Gruppe 3: Gesunde)

(Gruppe 1: Depressive, Gruppe 2: Remittierte, Gruppe 3: Gesunde)

Niveau ist abhängig von der Kodierung der Gruppe.
Ergebnis:
- Die Depressiven unterscheiden sich von den Remittierten signifikant.
- Die Depressiven unterscheiden sich von den Gesunden signifikant.
Tags: Kontrast
Source: VO02
Source: VO02
Was zeigt dieser SPSS Ausdruck?

(Gruppe 1: Depressive, Gruppe 2: Remittierte, Gruppe 3: Gesunde)

(Gruppe 1: Depressive, Gruppe 2: Remittierte, Gruppe 3: Gesunde)
Differenz (orthogonale Kontraste):
Ergebnis:
- Zuerst Vergleich Gruppe 2 (Remittierte) mit 1 (Depressive)
- Dann Vergleich Gruppe 3 vs. 1+2
Ergebnis:
- Die Depressiven unterscheiden sich von den Remittierten signifikant.
- Die Depressiven unterscheiden sich von den Gesunden signifikant.
Tags: Kontrast
Source: VO02
Source: VO02
Was zeigt dieser SPSS-Ausdruck?

(Gruppe 1: Depressive, Gruppe 2: Remittierte, Gruppe 3: Gesunde)

(Gruppe 1: Depressive, Gruppe 2: Remittierte, Gruppe 3: Gesunde)
Helmert (orthogonale Kontraste):
Ergebnis:
- Zuerst Vergleich Gruppe 1 (Depressive) vs. 2+3
- Dann Vergleich Gruppe 2 vs. 3
Ergebnis:
- Die Depressiven unterscheiden sich von den Remittierten signifikant.
- Die Depressiven unterscheiden sich von den Gesunden signifikant.
Tags: Kontrast
Source: VO02
Source: VO02
Was zeigt dieser SPSS-Ausdruck?

(Gruppe 1: Depressive, Gruppe 2: Remittierte, Gruppe 3: Gesunde)

(Gruppe 1: Depressive, Gruppe 2: Remittierte, Gruppe 3: Gesunde)

Wiederholt eignet sich, um sequenziell alle paarweisen Mittelwertsunterschiede zu testen (Gruppe1 mit Gruppe 2, Gruppe 2 und Gruppe 3, Gruppe 3 mit Gruppe 4)
Ergebnis:
- Die Depressiven unterscheiden sich von den Remittierten signifikant.
- Die Depressiven unterscheiden sich von den Gesunden signifikant.
Tags: Kontrast
Source: VO02
Source: VO02
Was sind Kontraste (im Überblick)?
- Einzelvergleiche (Kontraste) untersuchen, welche Gruppen sich signifikant voneinander unterscheiden Wenn die Varianzanalyse nicht signifikant war, dann ist es nicht sinnvoll die Kontraste zu untersuchen
- Einzelne Gruppen können auch gegenüber Kombinationen der anderen Gruppen kontrastiert werden
- Kontraste erlauben insbesondere auch die einseitige Hypothesenprüfung (wenn a priori spezifiziert)
- Polynomiale Trends in den (sinnvoll geordneten) Gruppenmittelwerten können statistisch untersucht werden
Tags: Kontrast
Source: VO02
Source: VO02
Was sind Post-hoc-Tests? Wofür sind die sinnvoll?
(Welche Gruppen unterscheiden sich voneinander - von der Zielsetzung gleich wie die Einzelvergleiche/Kontraste)
- Erlauben explorative Untersuchung, welche Gruppen sich nach signifikanten Omnibustest der ANOVA voneinander unterscheiden; vergleichen alle Paare von Gruppen miteinander (nicht-orthogonal)
- Nicht zur Testung von a priori Hypothesen, sondern zur Datenexploration
- Nur zweiseitige Tests ggf. geringere Testmacht als Einzelvergleiche/Kontraste bei Einzelvergleichen/Kontrasten erfolgt die ein-/zweiseitige Testung mittels der Betrachtung des p-Werts
- SPSS bietet Vielzahl (18!) an unterschiedlichen Post-Hoc-Testverfahren an - es ist nicht sofort klar welcher verwendet werden soll Unterschiede in der Art der Kontrolle des familywise error (Typ-I-Fehler), der Testmacht (Typ-II-Fehler) und der Robustheit gegenüber Voraussetzungsverletzungen
Tags: Post-hoc-Tests
Source: VO02
Source: VO02
Welcher Post-hoc-Tests ist anzuwenden wenn:
a) Gleiches n pro Gruppe und homogene Varianzen
b) Unterschiedliche ns und homogene Varianzen
c) Stark unterschiedliche ns und homogene Varianzen
d) Inhomogene Varianzen
a) Gleiches n pro Gruppe und homogene Varianzen
b) Unterschiedliche ns und homogene Varianzen
c) Stark unterschiedliche ns und homogene Varianzen
d) Inhomogene Varianzen
a) wenn Idealbedingungen der ANOVA zutreffen:
Q nach Ryan-Einot-Gabriel-Welsh
Tukey („Tukey‘s Honestly Significant Difference [HSD]“)
hohe Testmacht
b) Unterschiedliche Anzahl an Testpersonen (z.B. „doppelt so groß“) und Varianzen homogen:
Gabriel
c) Start unterschiedliche Anzahl an Testpersonen (z.B. „fünffach so groß“) und homogene Varianzen:
GT2 nach Hochberg
d) Inhomogene Varianzen:
Games-Howell

Q nach Ryan-Einot-Gabriel-Welsh
Tukey („Tukey‘s Honestly Significant Difference [HSD]“)
hohe Testmacht
b) Unterschiedliche Anzahl an Testpersonen (z.B. „doppelt so groß“) und Varianzen homogen:
Gabriel
c) Start unterschiedliche Anzahl an Testpersonen (z.B. „fünffach so groß“) und homogene Varianzen:
GT2 nach Hochberg
d) Inhomogene Varianzen:
Games-Howell

Tags: Post-hoc-Tests
Source: VO02
Source: VO02
Was zeigt dieser SPSS-Ausdruck?


Durchführung von 2 Arten der Post-Hoc-Tests:
- Q nach R-E-G-W und
- Gabriel (da leicht unterschiedliche n)
Mehrfachvergleiche = Gabriel
- Alle werden paarweise Verglichen
- Für jeden Vergleich wird das Signifikanzniveau angegeben.
Homogene Untergruppen: für Gabriel + Q nach REGW
Bestimmung homogener Untergruppen gemäß REGW-Q und Gabriel-Prozedur;
Jede Spalte unterscheidet sich von den anderen signifikant (p < .05); Bei mehr als einer Gruppe in einer Spalte gibt „Signifikanz“ das p des jeweiligen Gruppenunterschieds an (wenn p < .05 neue Spalte)
- Tabellarische Darstellung welche Gruppen sich signifikant voneinander unterscheiden (Alle Gruppen unterscheiden sich signifikant voneinander)
- Da die Zahlen aller Gruppen in einer eigenen Spalte sind unterscheiden sich alle Gruppen voneinander mit einer Wahrscheinlichkeit von 0,05.
Die Signifikanz ist immer 1. Die Signifikanz wird nur nicht 1 wenn mehrere Gruppen in einer Spalte sind (eine Gruppe unterscheidet sich von sich selbst gar nicht) und kann in diesem Fall ignoriert werden.
Hier noch ein Beispiel - wenn die Daten nicht alle voneinander signifikant unterschiedlich sind:

- Q nach R-E-G-W und
- Gabriel (da leicht unterschiedliche n)
Mehrfachvergleiche = Gabriel
- Alle werden paarweise Verglichen
- Für jeden Vergleich wird das Signifikanzniveau angegeben.
Homogene Untergruppen: für Gabriel + Q nach REGW
Bestimmung homogener Untergruppen gemäß REGW-Q und Gabriel-Prozedur;
Jede Spalte unterscheidet sich von den anderen signifikant (p < .05); Bei mehr als einer Gruppe in einer Spalte gibt „Signifikanz“ das p des jeweiligen Gruppenunterschieds an (wenn p < .05 neue Spalte)
- Tabellarische Darstellung welche Gruppen sich signifikant voneinander unterscheiden (Alle Gruppen unterscheiden sich signifikant voneinander)
- Da die Zahlen aller Gruppen in einer eigenen Spalte sind unterscheiden sich alle Gruppen voneinander mit einer Wahrscheinlichkeit von 0,05.
Die Signifikanz ist immer 1. Die Signifikanz wird nur nicht 1 wenn mehrere Gruppen in einer Spalte sind (eine Gruppe unterscheidet sich von sich selbst gar nicht) und kann in diesem Fall ignoriert werden.
Hier noch ein Beispiel - wenn die Daten nicht alle voneinander signifikant unterschiedlich sind:

Tags: Post-hoc-Tests
Source: VO02
Source: VO02
Was sind die Voraussetzungen für die Durchführung der einfaktoriellen ANOVA?
Annahmen und Voraussetzungen der Varianzanalyse
Gültigkeit und Durchführung der einfaktoriellen ANOVA sind an vier Voraussetzungen gebunden:
Gleiche Voraussetzungen wie t-Test !
Voraussetzungen müssen vor der Durchführung geprüft werden – bei Nicht-Zutreffen u. U. anderes Testverfahren (z.B. nicht-parametrisch)
Werden Voraussetzungen nicht erfüllt kann man auf nicht-parametrische Verfahren zurückgreifen oder eventuell trotzdem auf parametrische Verfahren wenn einzelne Voraussetzungen nicht erfüllt sind (Robustheit).
Gültigkeit und Durchführung der einfaktoriellen ANOVA sind an vier Voraussetzungen gebunden:
- Die abhängige Variable hat metrische Skaleneigenschaften (Intervallskala, Rationalskala)
- Die Gruppen sind voneinander unabhängig Es gibt keine Gruppe in der eine Person zweimal vorkommt
- Die Varianzen der untersuchten Gruppen sind homogen Varianz muss in den einzelnen Gruppen ungefähr gleich sein - Soll sich in der Varianzhomogenität zeigen
- Die Daten sind innerhalb der Gruppen normalverteilt
Gleiche Voraussetzungen wie t-Test !
Voraussetzungen müssen vor der Durchführung geprüft werden – bei Nicht-Zutreffen u. U. anderes Testverfahren (z.B. nicht-parametrisch)
Werden Voraussetzungen nicht erfüllt kann man auf nicht-parametrische Verfahren zurückgreifen oder eventuell trotzdem auf parametrische Verfahren wenn einzelne Voraussetzungen nicht erfüllt sind (Robustheit).
Tags: ANOVA, einfaktorielle ANOVA
Source: VO03
Source: VO03
Was ist das formale Modell der einfaktoriellen ANOVA?
Formales Modell der einfaktoriellen ANOVA


- Gesamtmittelwert und Effekt der Gruppe sind bloße Konstanten (feste Effekte [fixed effects]; Fehler haben Erwartungswert 0) Fixed effects model: man geht von fixen Effekten in einer Gruppe aus (d.h. jede Person variiert in einer Gruppe gleich – bzw. ist ein unterschiedliches Verhalten im Fehler abgebildet)
- Fehler haben einen Erwartungswert von 0 – d.h. es wird davon ausgegangen, dass der Fehler über alle Personen hinweg in der Gruppe 0 ist, sich die Fehler also ausgleichen.
- Streuungen in der Gruppe kommen NUR durch den Fehler zustande – deshalb muss eine Varianzhomogenität gegeben sein, damit sich diese Effekt ausgleichen. Fehler müssen sich in allen Gruppen gleich (Varianzhomogenität/Homoskedastizität) und normal verteilen
- Prüfung der Normalverteilung durch Kolmogorov-Smirnov- oder Shapiro-Wilk-Test (vgl. t-Test)
Tags: ANOVA, einfaktorielle ANOVA
Source: VO03
Source: VO03
Mit welchen Verfahren kann die Normalverteilung überprüft werden?
Prüfung der Normalverteilung durch Kolmogorov-Smirnov- oder Shapiro-Wilk-Test
(Notwendig als Voraussetzung z.B. für die einfaktorielle ANOVA, t-Test,...)

BDI-II-Scores bei Gesunden nicht normalverteilt (p < .05)
[H0 ist bei Voraussetzungstests „Wunschhypothese“ und soll beibehalten werden]
Box-Plots:
Verteilung bei Gesunden deutlich asymmetrisch (mehr niedrige als hohe Werte)
Keine Ausreißer

(Notwendig als Voraussetzung z.B. für die einfaktorielle ANOVA, t-Test,...)

BDI-II-Scores bei Gesunden nicht normalverteilt (p < .05)
[H0 ist bei Voraussetzungstests „Wunschhypothese“ und soll beibehalten werden]
Box-Plots:
Verteilung bei Gesunden deutlich asymmetrisch (mehr niedrige als hohe Werte)
Keine Ausreißer

- H0: Die Verteilung ist normalverteilt. H1: Die Verteilung ist nicht normalverteilt.
- D.h. man hofft auf ein nicht signifikantes Ergebnis. Bei den Gesunden ist das Ergebnis aber signifikant – d.h. die Gesunden sind nicht normalverteilt.
- Inhaltliche Info: Durch die Art der Messung tritt der Effekt (nicht normalverteilt) auf, da nach Symptomen gefragt wird und wenn man keine Symptome hat gibt man 0 an. Aber man kann nicht weniger als 0 angeben. Deshalb ist der Verteilung eher einseitig.
Tags: ANOVA, einfaktorielle ANOVA, Normalverteilung
Source: VO03
Source: VO03
Welche Methode kann für die Prüfung der Varianzhomogenität verwendet werden?
Prüfung der Varianzhomogenität durch Levene-Test (= Pendant des F-Test bei k > 2 Gruppen)

p > .05, also kann Varianzhomogenität angenommen werden;
[H0 ist „Wunschhypothese“ und soll beibehalten werden]
H0 – die Varianzen sind homogen.

p > .05, also kann Varianzhomogenität angenommen werden;
[H0 ist „Wunschhypothese“ und soll beibehalten werden]
H0 – die Varianzen sind homogen.
Tags: ANOVA, einfaktorielle ANOVA, Varianz, Varianzhomogenität
Source: VO03
Source: VO03
Was soll bei der Verletzung der Voraussetzung bei der einfaktoriellen ANOVA beachtet werden?
a) gleiches n, ungleiche NV und Varianzhomogenität
b) ungleiches n
c) keine Varianzhomogenität
a) gleiches n, ungleiche NV und Varianzhomogenität
b) ungleiches n
c) keine Varianzhomogenität
ANOVA ist ein robustes Verfahren, d.h. im Allgemeinen haben einzelne Voraussetzungsverletzungen keinen allzu großen Einfluss auf Ergebnis der Hypothesentestung.
a) Bei gleichen Stichprobengrößen sind Abweichungen von Normalverteilung oder der Varianzhomogenität häufig vernachlässigbar.
b) V. a. bei ungleichen ns können Abweichungen jedoch größeren Einfluss ausüben
c) Wenn Varianzen nicht homogen
zu b) + c) Beide Prozeduren wirksam in der Kontrolle des Typ-I-Fehlers, Welch kontrolliert i. A. aber den Typ-II-Fehler besser (höhere Testmacht; vgl.
Field, 2009)

Da die ANOVA ein robustes Verfahren ist – kann die ANOVA bei diesem Beispiel trotzdem angewendet werden, auch wenn bei einer Gruppe die Normalverteilung nicht gegeben ist.
Dies ist auch abhängig von der Stichprobengröße.
Wenn man nicht sicher ist – kann man das nicht-parametrische Verfahren anwenden und dann mit dem Ergebnis der parametrischen Verfahren zu vergleichen. Sind die Ergebnisse gleich/ähnlich so kann das parametrische Verfahren verwendet werden.
a) Bei gleichen Stichprobengrößen sind Abweichungen von Normalverteilung oder der Varianzhomogenität häufig vernachlässigbar.
b) V. a. bei ungleichen ns können Abweichungen jedoch größeren Einfluss ausüben
- keine ausreichende Kontrolle von Typ-I- und Typ-II-Fehlerraten
- u. U. Ausweichen auf nicht-parametrische Tests
c) Wenn Varianzen nicht homogen
- robuster F-Test: Korrektur nach Brown-Forsythe oder Welch
- Korrigieren Freiheitsgrade des Fehlers (dfInnerhalb) und beruhen auf alternativer Berechnung der Quadratsummen
zu b) + c) Beide Prozeduren wirksam in der Kontrolle des Typ-I-Fehlers, Welch kontrolliert i. A. aber den Typ-II-Fehler besser (höhere Testmacht; vgl.
Field, 2009)

Da die ANOVA ein robustes Verfahren ist – kann die ANOVA bei diesem Beispiel trotzdem angewendet werden, auch wenn bei einer Gruppe die Normalverteilung nicht gegeben ist.
Dies ist auch abhängig von der Stichprobengröße.
Wenn man nicht sicher ist – kann man das nicht-parametrische Verfahren anwenden und dann mit dem Ergebnis der parametrischen Verfahren zu vergleichen. Sind die Ergebnisse gleich/ähnlich so kann das parametrische Verfahren verwendet werden.
Tags: ANOVA, einfaktorielle ANOVA
Source: VO03
Source: VO03
Was zeigt dieser SPSS-Ausdruck?


Eine Voraussetzung für die Durchführung der einfaktoriellen ANOVA ist die Varianzhomogenität.
Wenn Varianzen nicht homogen:
Aufruf in SPSS:

Ergebnis:

oben: Tabelle zur Varianzanalyse
unten: df1 = 2 Freiheitsgrade (3 Gruppen - 1)
df2 wurde von 104 nach unten korrigiert - es hat sich nicht viel geändert, da die Varianzen homogen waren
Wenn Varianzen nicht homogen:
- robuster F-Test: Korrektur nach Brown-Forsythe oder Welch
- Korrigieren Freiheitsgrade des Fehlers (dfInnerhalb) und beruhen auf alternativer Berechnung der Quadratsummen
Aufruf in SPSS:

Ergebnis:

oben: Tabelle zur Varianzanalyse
unten: df1 = 2 Freiheitsgrade (3 Gruppen - 1)
df2 wurde von 104 nach unten korrigiert - es hat sich nicht viel geändert, da die Varianzen homogen waren
Tags: ANOVA, einfaktorielle ANOVA, SPSS
Source: VO03
Source: VO03
Was testen mehrfaktorielle ANOVA (factorial ANOVA)?
Mehrfaktorielle ANOVAs testen
Im Folgenden wird der Spezialfall (einfachste Fall) der zweifaktoriellen ANOVA mit jeweils zwei Stufen pro Faktor behandelt.
Allgemein ist der Anzahl der Faktoren und ihrer Stufen (im Prinzip) bei ausreichend großen Stichproben keine Grenze gesetzt.
- Haupteffekte (Effekte einzelner Faktoren unabhängig von allen anderen Faktoren) und
- Wechselwirkungen (Effekte spezifischer Faktorstufenkombinationen)
Im Folgenden wird der Spezialfall (einfachste Fall) der zweifaktoriellen ANOVA mit jeweils zwei Stufen pro Faktor behandelt.
Allgemein ist der Anzahl der Faktoren und ihrer Stufen (im Prinzip) bei ausreichend großen Stichproben keine Grenze gesetzt.
Tags: mehrfaktorielle ANOVA, zweifaktorielle ANOVA
Source: VO03
Source: VO03
Tags: zweifaktorielle ANOVA
Source: VO03
Source: VO03
Welche Hypothesen werden bei der zweifaktoriellen ANOVA überprüft?
Drei F-Tests (einer je Haupteffekt, einer für die Wechselwirkung)

3 Nullhypothesen (Folie 3)

Wechselwirkung liegt dann vor, wenn der Effekt verschiedener Faktorstufenkombinationen nicht additiv ist
Beispiel
Zeigen sich Geschlechts-Unterschiede in Trait-Angst (STAI) in gleicher Weise, unabhängig vom Vorliegen einer Angststörung?

Beispiel – 2 Faktoren: Geschlecht (männlich und weiblich), Population (normal, Angststörung)
Folie 5: Haupteffekte sind signifikant (Geschlechtsunterschiede sind signifikant und Gruppenunterschiede sind signifikant), aber Wechselwirkung ist nicht signifikant.
Folie 7: 2 Nahezu parallele Linien – deshalb keine Wechselwirkung


3 Nullhypothesen (Folie 3)
- Ersten zwei Hypothesen: Es gibt keinen Unterschied zwischen den Mittelwerten – untersucht ob die Gruppen gleich oder ungleich sind jeweils für die Faktoren
- Wechselwirkung (Effekte die über additive Effekte hinausgeht): Der Mittelwert in einer Faktorstufenkombination: Mittelwert Faktor 1 + Mittelwert Faktor 2 - Gesamtmittelwert (Die Formel/H0 beschreibt, dass es nur einen additiven Effekt gibt)

Wechselwirkung liegt dann vor, wenn der Effekt verschiedener Faktorstufenkombinationen nicht additiv ist
Beispiel
Zeigen sich Geschlechts-Unterschiede in Trait-Angst (STAI) in gleicher Weise, unabhängig vom Vorliegen einer Angststörung?

Beispiel – 2 Faktoren: Geschlecht (männlich und weiblich), Population (normal, Angststörung)
Folie 5: Haupteffekte sind signifikant (Geschlechtsunterschiede sind signifikant und Gruppenunterschiede sind signifikant), aber Wechselwirkung ist nicht signifikant.
Folie 7: 2 Nahezu parallele Linien – deshalb keine Wechselwirkung

Tags: zweifaktorielle ANOVA
Source: VO03
Source: VO03
Was zeigt dieser SPSS-Ausdruck?


Beispiel: Zeigen sich Geschlechts-Unterschiede in Trait-Angst (STAI) in gleicher Weise, unabhängig vom Vorliegen einer Angststörung?

2 Faktoren: Geschlecht (männlich und weiblich), Population (normal, Angststörung)
SPSS-Ausdruck zeigt: Haupteffekte sind signifikant (Geschlechtsunterschiede sind signifikant und Gruppenunterschiede sind signifikant), aber Wechselwirkung ist nicht signifikant.
Folie 7: 2 Nahezu parallele Linien – deshalb keine Wechselwirkung


2 Faktoren: Geschlecht (männlich und weiblich), Population (normal, Angststörung)
- Haupteffekte Geschlecht und Gruppe jeweils signifikant (p < .05);
- Wechselwirkung Geschlecht*Gruppe nicht signifikant (p = .808)
- [NV in allen 4 Gruppen gegeben (Shapiro-Wilk-Tests, ps ≥ .450)]
SPSS-Ausdruck zeigt: Haupteffekte sind signifikant (Geschlechtsunterschiede sind signifikant und Gruppenunterschiede sind signifikant), aber Wechselwirkung ist nicht signifikant.
Folie 7: 2 Nahezu parallele Linien – deshalb keine Wechselwirkung

Tags: zweifaktorielle ANOVA
Source: VO03
Source: VO03
Was zeigt die grafische Darstellung hinsichtlich der Wechselwirkung (zweifaktorielle ANOVA)?

Diagramm verdeutlicht, dass Effekte additiv sind - es liegt keine Wechselwirkung vor;
Effekt des Geschlechts ist über beide Stufen von Gruppe gleich.

Ebenso ist der Effekt von Gruppe über beide Geschlechter gleich.

..... Parallele Linien, keine Wechselwirkung

Effekt des Geschlechts ist über beide Stufen von Gruppe gleich.

Ebenso ist der Effekt von Gruppe über beide Geschlechter gleich.

..... Parallele Linien, keine Wechselwirkung

Tags: zweifaktorielle ANOVA
Source: VO03
Source: VO03
Welchen Einfluss hat eine signifikante Wechselwirkung (einer zweifaktoriellen ANOVA) auf die Interpretation der Haupteffekte?
Wie ist dies bei mehrfaktoriellen Untersuchungen und welche Methode kann hir eingesetzt werden?
Wie ist dies bei mehrfaktoriellen Untersuchungen und welche Methode kann hir eingesetzt werden?
Ist die Wechselwirkung signifikant, kann dies Einfluss auf die Interpretierbarkeit gleichzeitig signifikanter Haupteffekte haben
Kann mittels mehrfacher Profilplots geklärt werden Klassifikation ordinaler, hybrider und disordinaler Interaktionen
Von der Klassifikation dieser Profilplots ist abhängig, ob signifikante Haupteffekte interpretiert werden dürfen
Mehrfaktorielle Untersuchungen
Interpretation von Wechselwirkungen wird komplexer und
anspruchsvoller bei
Mittels Kontrasttests kann dann ermittelt werden, wo Wechselwirkungen liegen (simple effects analysis; in SPSS nur via Syntax)
Simple effects analysis prüft Gruppenunterschiede in einem Faktor für jede einzelne Stufe des/eines anderen Faktors.
Alternativ können auch Konfidenzintervalle herangezogen werden.
Kann mittels mehrfacher Profilplots geklärt werden Klassifikation ordinaler, hybrider und disordinaler Interaktionen
- Ein Profilplot, wo für Faktor A über Faktor B separate Linien gezogen werden
- Ein zweiter, wo für Faktor B über Faktor A separate Linien gezogen werden
Von der Klassifikation dieser Profilplots ist abhängig, ob signifikante Haupteffekte interpretiert werden dürfen
- Ordinale Interaktion: beide Haupteffekte interpretierbar
- Hypride Interaktion: nur ein Haupteffekt interpretierbar
- Disordinale Interaktion: kein Haupteffekt interpretierbar
Mehrfaktorielle Untersuchungen
Interpretation von Wechselwirkungen wird komplexer und
anspruchsvoller bei
- mehr als zwei Stufen pro Faktor
- mehr als zwei Faktoren (nicht nur einfache Interaktionen, sondern auch zweifache und dreifache, etc.)
Mittels Kontrasttests kann dann ermittelt werden, wo Wechselwirkungen liegen (simple effects analysis; in SPSS nur via Syntax)
Simple effects analysis prüft Gruppenunterschiede in einem Faktor für jede einzelne Stufe des/eines anderen Faktors.
Alternativ können auch Konfidenzintervalle herangezogen werden.
Tags: Haupteffekte, Interaktion, zweifaktorielle ANOVA
Source: VO03
Source: VO03
Was versteht man unter der ordinalen Interaktion? Können die Haupteffekte interpretiert werden?

Linienzüge zeigen in beiden Diagrammen gleiche Trends (steigend) .... dann sind beide Haupteffekte (wenn signifikant) interpretierbar (a1 < a2, b1 < b2), Wechselwirkung wirkt quasi „verstärkend“ auf Haupteffekte ein (die Differenz b1-b2 ist in a1 kleiner als in a2)
Beide Linien folgen dem GLEICHEN Trend (die Wechselwirkung wirkt verstärkend) - Haupteffekte dürfen als bedeutsam interpretiert werden.
Tags: Haupteffekt, Interaktion, zweifaktorielle ANOVA
Source: VO03
Source: VO03
Was versteht man unter der hybriden Interaktion? Können die Haupteffekte interpretiert werden?

Linienzüge zeigen im linken Diagramm (Faktor A) gegenläufige Trends, überkreuzte, aber immer noch gleichsinnige Linienzüge im rechten Diagramm (Faktor B)
... nur Haupteffekt B (wenn signifikant) interpretierbar (b1 < b2), aber a1 > a2 in b1 und a1 < a2 in b2
GEGENLÄUFIGE Trends (Faktor A) und GLEICHSINNIGE Trends (Faktor B) - Haupteffekt (wenn vorhanden) darf bei Faktor A nicht interpretiert werden; für Faktor B darf der Haupteffekt noch immer interpretiert werden
Tags: Interaktion, Wechselwirkung, zweifaktorielle ANOVA
Source: VO03
Source: VO03
Was versteht man unter der disordinalen Interaktion? Können die Haupteffekte interpretiert werden?

Linienzüge in beiden Diagrammen überkreuzt - kein Haupteffekt (wenn signifikant) ist für sich genommen interpretierbar
beide Trends sind GEGENLÄUFIG - Beide Haupteffekte dürfen nicht interpretiert werden, da es keinen Haupteffekt gibt, sondern nur auf die Faktorenstufen in Kombination ankommt.
Tags: Interaktion, Wechselwirkung, zweifaktorielle ANOVA
Source: VO03
Source: VO03
Was kann mit der simple effects analysis überprüft werden? Wie wird diese in SPSS durchgeführt?
Mittels Kontrasttests kann bei mehrfaktorieller ANOVA ermittelt werden, wo Wechselwirkungen liegen (simple effects analysis).
Simple effects analysis prüft Gruppenunterschiede in einem Faktor für jede einzelne Stufe des/eines anderen Faktors.

Ergebnis

Paarweise Vergleiche:
Test auf Geschlechtsunterschiede innerhalb der Stufen: nicht signifikant bei Gesunden, signifikant bei Angststörung

CAVE: Wechselwirkung war nicht signifikant (p = .808 - aus Vorwissen/anderer Tabelle)
Simple effects analysis prüft Gruppenunterschiede in einem Faktor für jede einzelne Stufe des/eines anderen Faktors.

- Definiert ein ALM (allgemeines lineares Modell - GLM) mit der abhängigen Variable STAI_trait und den Faktoren Geschlecht und Gruppe
- Spezifikation der simple effects analysis: TABLES(…) definiert die beiden Faktoren, die getestet werden sollen; COMPARE(Geschlecht) gibt an, dass der Effekt des Geschlechts innerhalb der Stufen des anderen Faktors (Gruppe) untersucht werden soll
Ergebnis

Paarweise Vergleiche:
Test auf Geschlechtsunterschiede innerhalb der Stufen: nicht signifikant bei Gesunden, signifikant bei Angststörung

CAVE: Wechselwirkung war nicht signifikant (p = .808 - aus Vorwissen/anderer Tabelle)
- Unterschied in Signifikanz bei Gesunden und Angststörung wird nicht interpretiert (Wechselwirkung)
- Haupteffekt des Geschlechtes wird interpretiert (p = .010)
Tags: Interaktion, mehrfaktorielle ANOVA, Wechselwirkung, zweifaktorielle ANOVA
Source: VO03
Source: VO03
Was kann statt der simple effects analysis verwendet werden um bei Wechselwirkungen die Interpretierbarkeit der Haupteffekte festzustellen?
Verwendung der Konfidenzintervalle (KIs)

Die Konfidenzintervalle überlappen sich.
Auch hier CAVE: Innerhalb von Gruppe überlappen sich hier die KIs von Frauen und Männern .... doch kein Haupteffekt Geschlecht ?
Doch! Test des Haupteffekts geht über alle Stufen der anderen Faktoren mehr Testmacht als KIs!

Die Konfidenzintervalle überlappen sich.
Auch hier CAVE: Innerhalb von Gruppe überlappen sich hier die KIs von Frauen und Männern .... doch kein Haupteffekt Geschlecht ?
Doch! Test des Haupteffekts geht über alle Stufen der anderen Faktoren mehr Testmacht als KIs!
Tags: Konfidenzintervall, zweifaktorielle ANOVA
Source: VO03
Source: VO03
Wann darf die simple effects analysis oder die KIs zur Untersuchung der Haupteffekte nur eingesetzt werden (mehrfaktorielle ANOVA)?
Simple effects analysis oder KIs nur dann heranziehen, wenn die
Wechselwirkung in der ANOVA signifikant ausfiel.
Wechselwirkung in der ANOVA signifikant ausfiel.
Tags: Konfidenzintervall, mehrfaktorielle ANOVA, zweifaktorielle ANOVA
Source: VO03
Source: VO03
Was sind die Voraussetzungen für die zweifaktorielle ANOVA?
- Voraussetzungen der zweifaktoriellen (und mehrfaktoriellen) ANOVA sind dieselben wie für einfaktorielle ANOVA: - metrische Daten,- Unabhängigkeit,- Varianzhomogenität,- Normalverteilung)
- Achtung: Voraussetzung der Normalverteilung muss in allen Faktorstufenkombinationen (= Gruppen) untersucht werden! - Bei 2 Faktoren mit jeweils 2 Stufen 4 Gruppen
- Mehrfaktorielle ANOVA i.A. wie einfaktorielle ANOVA ebenso robust
- Es gibt jedoch keinen vergleichbaren nicht-parametrischen Test in SPSS (z.B. zweifaktorielle Rangvarianzanalyse nicht in SPSS implementiert)
WICHTIG: Alle 4 Varianzen müssen homogen sein (2 Faktoren mit jeweils 2 Stufen)
Alle 4 Gruppen müssen jeweils normalverteilt sein.
Tags: zweifaktorielle ANOVA
Source: VO03
Source: VO03
Was zeigt dieser SPSS-Ausdruck?


Dieser zeigt eine NV-Testung über alle Faktorstufenkombinationen (bei einem zweifaktoriellen Design)
(Für alle Gruppen gilt die Normalverteilung - keine signifikanten Ergebnisse)
(Für alle Gruppen gilt die Normalverteilung - keine signifikanten Ergebnisse)
Tags: mehrfaktorielle ANOVA, Normalverteilung, zweifaktorielle ANOVA
Source: VO03
Source: VO03
Was ist bei der Anwendung von Kontrasten und Post-hoc-Tests bei zwei- bzw. mehrfaktoriellen Designs zu beachten?
Kontraste (voreingestellte) und Post-Hoc-Tests können ebenso wie in einfaktorieller ANOVA verwendet werden.
Sie testen in der factorial ANOVA ebenso Hypothesen jeweils über einen Faktor und lassen die anderen Faktoren unberücksichtigt.
Kontraste und Post-Hoc-Test können auch angewendet werden – jedoch wird immer nur ein Faktor berücksichtigt (und andere Faktoren werden nicht berücksichtigt). Dies kann also nur sinnvoll verwendet werden wenn es keine Wechselwirkungen zwischen den Faktoren gibt. Wenn es Wechselwirkungen gibt kann es zu verzerrten Ergebnissen kommen.
Sie testen in der factorial ANOVA ebenso Hypothesen jeweils über einen Faktor und lassen die anderen Faktoren unberücksichtigt.
- kann inadäquat sein, wenn Wechselwirkungen vorliegen
- simple effect analysis wird dann benötigt
Kontraste und Post-Hoc-Test können auch angewendet werden – jedoch wird immer nur ein Faktor berücksichtigt (und andere Faktoren werden nicht berücksichtigt). Dies kann also nur sinnvoll verwendet werden wenn es keine Wechselwirkungen zwischen den Faktoren gibt. Wenn es Wechselwirkungen gibt kann es zu verzerrten Ergebnissen kommen.
Tags: Kontrast, mehrfaktorielle ANOVA, Post-Hoc-Test, zweifaktorielle ANOVA
Source: VO03
Source: VO03
Was sind abhängige Daten? Wie entstehen abhängige Daten?
- Abhängige Daten in psychologischer und insbesondere klinischer Forschung häufig
- Alle Interventionsstudien analysieren im Prinzip abhängige Daten (Prä-/Postvergleiche [Datenerhebungen vor und nach Interventionen])
- Abhängige Daten entstehen allgemein – durch Messwiederholung– durch Parallelisierung (matched samples)– bei Untersuchung natürlicher Paare (z.B. Geschwister, Ehepaare)
- Verwendung abhängiger Daten verringert i. A. Zufallsfehler ... Testmacht steigt durch Elimination interindividueller Unterschiede (bei Messwiederholungen: „Jede Vpn ist ihre eigene Kontrolle“)
Was sind abhängige Daten?
- Längsschnittstudie: Z.B. Daten die von der gleichen Person zu unterschiedlichen Zeitpunkten erhoben wurden.
- Parallelisierung: Wenn man Personen sucht die vergleichbar sind. Man ordnet Personen einander zu und erhält dadurch abhängige Daten
- Natürliche Paare von Personen – z.B. Geschwister, Eltern, Ehepaar
Vorteil abhängiger Daten: verringert den Zufallsfehler. Dadurch steigt die Testmacht (eher signifikantes Ergebnis)
Einfachster Fall abhängiger Daten: 2 Messungen t-Test für abhängige Stichproben
Tags: abhängige Daten
Source: VO03
Source: VO03
Was untersucht ein t-Test abhängiger Stichproben?
Einfachster Fall abhängiger Daten:
2 Messungen ... t-Test für abhängige Stichproben
Test untersucht nicht wie im Fall unabhängiger Stichproben, ob sich die Mittelwerte zweier Verteilungen voneinander unterscheiden, sondern ob der Mittelwert der Differenz aller Messwertpaare ungleich 0 ist.
Abhängiger t-Test ist Test über die


Beispiel: (angelehnt an Keller et al., 2000)
Gibt es einen kombinierten Effekt bei einer Behandlung von Psychopharmaka und therapeutischer (Verhaltenstherapie – CBT) Behandlung.
Effekt einer kognitiv-behavioralen Depressionsbehandlung (CBT)
N = 56 depressive Patienten vor und nach der 12-wöchigen Behandlung

2 Messungen ... t-Test für abhängige Stichproben
Test untersucht nicht wie im Fall unabhängiger Stichproben, ob sich die Mittelwerte zweier Verteilungen voneinander unterscheiden, sondern ob der Mittelwert der Differenz aller Messwertpaare ungleich 0 ist.
Abhängiger t-Test ist Test über die


Beispiel: (angelehnt an Keller et al., 2000)
Gibt es einen kombinierten Effekt bei einer Behandlung von Psychopharmaka und therapeutischer (Verhaltenstherapie – CBT) Behandlung.
Effekt einer kognitiv-behavioralen Depressionsbehandlung (CBT)
N = 56 depressive Patienten vor und nach der 12-wöchigen Behandlung

Tags: abhängige Daten, t-Test
Source: VO03
Source: VO03
Was sind die Voraussetzungen für die Durchführung des t-Tests für abhängige Stichproben?
Test untersucht nicht wie im Fall unabhängiger Stichproben, ob sich die Mittelwerte zweier Verteilungen voneinander unterscheiden, sondern ob der Mittelwert der Differenz aller Messwertpaare ungleich 0 ist.
Abhängiger t-Test ist Test über die

Voraussetzungen:
Abhängiger t-Test ist Test über die

Voraussetzungen:
- Metrische Daten (Intervall-, Rationalskala)
- Abhängige Messungen
- Normalverteilung der Differenzen di
- t-Test abhängiger Stichproben: Normalverteilung muss innerhalb der berechneten Differenzen vorhanden sein
- t-Test unabhängiger Stichproben: Normalverteilung muss in jeder der beiden Gruppen vorliegen
Tags: abhängige Daten, t-Test
Source: VO03
Source: VO03
Was zeigt dieser SPSS-Ausdruck?




Beispiel: (angelehnt an Keller et al., 2000)
Effekt einer kognitiv-behavioralen Depressionsbehandlung (CBT)
N = 56 depressive Patienten vor und nach der 12-wöchigen Behandlung
Gibt es einen kombinierten Effekt bei einer Behandlung von Psychopharmaka und therapeutischer (Verhaltenstherapie – CBT) Behandlung.

Ausdruck zeigt t-Test mit abhängigen Daten: Intervention hochsignifikant wirksam
(H0 war: Differenzen unterscheiden sich nicht)
- Korrelation: Personen mit hohen Werten zu Beginn hatten auch am Ende hohe Werte.
- t-Test: t = 13, 658, Df = 55 – ist statistisch signifikant.
Effekt einer kognitiv-behavioralen Depressionsbehandlung (CBT)
N = 56 depressive Patienten vor und nach der 12-wöchigen Behandlung
Gibt es einen kombinierten Effekt bei einer Behandlung von Psychopharmaka und therapeutischer (Verhaltenstherapie – CBT) Behandlung.

Ausdruck zeigt t-Test mit abhängigen Daten: Intervention hochsignifikant wirksam
(H0 war: Differenzen unterscheiden sich nicht)
- Korrelation: Personen mit hohen Werten zu Beginn hatten auch am Ende hohe Werte.
- t-Test: t = 13, 658, Df = 55 – ist statistisch signifikant.
Tags: abhängige Daten, t-Test
Source: VO03
Source: VO03
Wie muss vorgegangen werden um die Voraussetzung der Normalverteilung für den t-Test abhängiger Stichproben zu untersuchen?
t-Test abhängiger Stichproben: Normalverteilung muss innerhalb der berechneten Differenzen vorhanden sein
Zur Überprüfung der Voraussetzungen (NV) muss neue Variable berechnet werden - Messwertdifferenzen !!!
Für diese neue Variable muss die Normalverteilung überprüft werden: Diff als abhängige Variable wählen.

Zur Überprüfung der Voraussetzungen (NV) muss neue Variable berechnet werden - Messwertdifferenzen !!!
Für diese neue Variable muss die Normalverteilung überprüft werden: Diff als abhängige Variable wählen.

Tags: abhängige Daten, Normalverteilung, t-Test
Source: VO03
Source: VO03
Was wird mit einer mixed ANOVA untersucht?
In ANOVA kann Einfluss sowohl unabhängiger als auch abhängiger Faktoren (simultan) untersucht werden.
„Klassisches“ Design der Interventionsforschung .... mixed design; mixed ANOVA
„Klassischer“ Anwendungsfall wird im Folgenden behandelt (2 Stufen im Zwischensubjektfaktor, 2 Stufen im Innersubjektfaktor)
In mixed ANOVA wird zwischen zwei Fehlertermen, zwei Quellen der Fehlervarianz, unterschieden:

Wechselwirkung zwischen unabhängigem und abhängigem Faktor kann getestet werden
- Residuum: Fehlerterm der intraindividuellen Variabilität, konfundiert mit Interaktionseffekten (jede Vpn × jede Stufe des abhängigen Faktors)

F-Test für ZSF anhand der Varianzschätzung durch QSFehler, für ISF und Wechselwirkung anhand jener von QSRes.
Beispiel:
Wirkung von CBT im Vergleich zu CBT + Antidepressivum in Depressionsbehandlung (RCT: Randomized Controlled Trial)

„Klassisches“ Design der Interventionsforschung .... mixed design; mixed ANOVA
- Ein Zwischensubjektfaktor (unabhängig; z.B. Versuchs- und Kontrollgruppe)
- Ein Innersubjektfaktor (abhängig; z.B. Prä-/Postmessung)
„Klassischer“ Anwendungsfall wird im Folgenden behandelt (2 Stufen im Zwischensubjektfaktor, 2 Stufen im Innersubjektfaktor)
In mixed ANOVA wird zwischen zwei Fehlertermen, zwei Quellen der Fehlervarianz, unterschieden:
- unsystematische Variabilität innerhalb der Stufen des unabhängigen Faktors
- unsystematische Variabilität innerhalb der Stufen des abhängigen Faktors

Wechselwirkung zwischen unabhängigem und abhängigem Faktor kann getestet werden
- Residuum: Fehlerterm der intraindividuellen Variabilität, konfundiert mit Interaktionseffekten (jede Vpn × jede Stufe des abhängigen Faktors)

F-Test für ZSF anhand der Varianzschätzung durch QSFehler, für ISF und Wechselwirkung anhand jener von QSRes.
Beispiel:
Wirkung von CBT im Vergleich zu CBT + Antidepressivum in Depressionsbehandlung (RCT: Randomized Controlled Trial)

Tags: mixed ANOVA
Source: VO04
Source: VO04
Was zeigen die SPSS-Ausdrucke zur mixed ANOVA?










- Deskriptive Statistik - vorläufig nicht notwendig
- Box-Test auf Gleicheit der Kovarianzmatrizen: Voraussetzungstest der MANOVA (nicht näher relevant für mixed ANOVA)
- Tafel Multivariate Tests (nicht in Screenshots) ebenso ignorieren - Output weiter unten ansehen …
- Mauchly-Test auf Sphärizität: Spezieller Voraussetzungstest der ANOVA mit Mess-WH; Nur relevant, wenn abhängiger Faktor > 2 Stufen hat
- Tests der Innersubjekteffekte: Abhängiger Faktor Zeit und Wechselwirkung ist signifikant (ps < .001) .... Haupteffekt Behandlung ? Tests der Innersubjekteffekte:- Die 3 Zeilen unter der markierten Ebene sind relevant wenn die Sphärizität verletzt ist.- Fehler in der Zeit = ResiduumInterpretation: Beide Effekte sind signifikant, aber es gibt auch große Wechseleffekte
- Levene Test: Levene-Tests für Vergleich der Stufen des unabhängigen Faktors innerhalb jeder Stufe des abhängigen Faktors Homogenität gegeben (ps > .05)
- Tests der Zwischensubjekteffekte: Haupteffekt Behandlung (gemittelt über beide Zeitpunkte) nicht signifikant (p > .05) Der Zwischensubjekteffekt zeigt, dass gemittelt über die Messungen kein signifikantes Ergebnis gibt.
- Behandlung * Zeit: KIs überschneiden sich zum ersten Zeitpunkt, aber nicht zum zweiten Zeitpunkt (niedrigere [= bessere] Werte in Gruppe CBT + Med) Differentieller Effekt der T2 = Dies bedeutet das es in der 2. Gruppe einen stärkeren, signifikanten Rückgang gibt als in der ersten Gruppe.
Tags: mixed ANOVA
Source: VO04
Source: VO04
Was zeigt dieser Profilplot der mixed ANOVA?


- Profilplot verdeutlicht, dass Behandlung mit CBT + Med größeren Effekt hat als mit CBT alleine
- Keine Baseline-Unterschiede, aber differentieller Effekt zu T2, der durch signifikante Wechselwirkung belegt wird
Tags: mixed ANOVA
Source: VO04
Source: VO04
Was zeigt dieser SPSS-Ausdruck?






Simple Effekts analysis – Anwendung mit mixed design ANOVA
Hat jede einzelne Behandlungsart für sich auch zu einem Rückgang der Depression geführt?

Test auf Behandlungsunterschiede innerhalb der Stufen:
Durchführung einer 2. simple effects analysis
mit Bezug auf die Zeit (COMPARE(Zeit)).
Test der jeweiligen Behandlungseffekte: beide Behandlungen führen zu einem signifikanten Rückgang der Depressivität

Interpretation:
Hat jede einzelne Behandlungsart für sich auch zu einem Rückgang der Depression geführt?

- 1. Zeile: Definiert ein ALM (allgemeine lineare Modell) mit der abhängigen Variablen HRSD_baseline und HRSD_post_treatment (= Stufen des abhängigen Faktors) und dem unabhängigen Faktor Behandlung
- 2. Zeile: Definiert, dass der abhängige (= Messwiederholungs-)Faktor Zeit heißt und 2 Stufen hat
- 3. Zeile: Spezifikation der simple effects analysis: TABLES(…) definiert die beiden Faktoren, die getestet werden sollen; COMPARE(Behandlung) gibt an, dass der Effekt der Behandlung innerhalb der Stufen des anderen Faktors (Zeit) untersucht werden soll
Test auf Behandlungsunterschiede innerhalb der Stufen:
- nicht signifikant zur Baseline, signifikant nach der Behandlung
- Da Wechselwirkung signifikant (p < .001), wird dies nun interpretiert - Patienten unterschieden sich nicht zur Baseline (p = .057)- Nach der Behandlung hatte jedoch die Gruppe CBT + Med niedrigere Werte als Gruppe CBT (p < .001)
Durchführung einer 2. simple effects analysis
mit Bezug auf die Zeit (COMPARE(Zeit)).
Test der jeweiligen Behandlungseffekte: beide Behandlungen führen zu einem signifikanten Rückgang der Depressivität

Interpretation:
- Beide Treatments waren wirksam in der Behandlung der Depression (Haupteffekt Zeit, p < .001; gleichermaßen signifikante Effekte in der simple effects analysis)
- Die Wirksamkeit der Treatments unterschied sich jedoch (Wechselwirkung, p < .001)
- Während zur Baseline beide Behandlungsgruppen vergleichbar hinsichtlich ihrer Depressivität waren (simple effects analysis; Zeitpunkt 1: p = .057), hatten die Patienten der Gruppe CBT + Med nach Beendigung der Behandlung niedrigere Werte als die Patienten der Gruppe CBT (Zeitpunkt 2: p < .001)
Tags: Haupteffekt, mixed ANOVA, simple effects analysis
Source: VO04
Source: VO04
Was sind die Voraussetzungen (5) der mixed ANOVA?
- Metrische Daten (Intervall-, Rationalskala)
- Unabhängige Gruppen, an denen zumindest zwei (abhängige) Messungen vorgenommen werden
- Varianzhomogenität (innerhalb der Stufen des abhängigen Faktors)
- Sphärizität (nur bei mehr als zwei Stufen im abhängigen Faktor)
- Multivariate Normalverteilung (innerhalb der Stufen des unabhängigen Faktors)
Tags: mixed ANOVA
Source: VO04
Source: VO04
Wie kann die multivariate Normalverteilung (als Voraussetzung für die mixed ANOVA) überprüft werden?
Multivariate Normalverteilung (innerhalb der Stufen des
unabhängigen Faktors):
kann mit SPSS nicht direkt geprüft werden
Näherungsweise durch Überprüfung der univariaten NV (jede Gruppe in jeder abhängigen Messung) bei Geltung der multivariaten NV ist auch jede Variable univariat normalverteilt (Umkehrschluss gilt jedoch nicht !!!)
unabhängigen Faktors):
kann mit SPSS nicht direkt geprüft werden
Näherungsweise durch Überprüfung der univariaten NV (jede Gruppe in jeder abhängigen Messung) bei Geltung der multivariaten NV ist auch jede Variable univariat normalverteilt (Umkehrschluss gilt jedoch nicht !!!)
Tags: mixed ANOVA
Source: VO04
Source: VO04
Was versteht man unter Sphärizität und wie kann diese überprüft werden?
(Sphärizität ist eine Voraussetzung für die mixed ANOVA)
Sphärizität (= Zirkularität):

Erübrigt sich für den Fall bloß zweier abhängiger Messungen

Wenn man nur 2 abhängige Messungen hat, dann gibt es nur 1 Differenz (die ist natürlich mit sich selbst identisch) und deshalb muss bei 2 Messungen keine Sphärizität überprüft werden.
Sphärizität (= Zirkularität):
- Mauchly-Test (wenn p > .05 ... Sphärizität gegeben)
- Annahme, dass die Varianzen der Differenzen aller Paare von abhängigen Messungen gleich sind (bedeutet, dass die einzelnen Varianzen und Kovarianzen gleich sind.)

Erübrigt sich für den Fall bloß zweier abhängiger Messungen

Wenn man nur 2 abhängige Messungen hat, dann gibt es nur 1 Differenz (die ist natürlich mit sich selbst identisch) und deshalb muss bei 2 Messungen keine Sphärizität überprüft werden.
Tags: MANOVA, mixed ANOVA, Sphärizität
Source: VO04
Source: VO04
Was kann getan werden wenn die Sphärizität verletzt ist?
Was tun bei Verletzung? (Mauchly-Test signifikant)
... Greenhouse-Geisser- und Huynh-Feldt-Korrekturen: Bestimmung eines Faktors Epsilon zur Korrektur der Freiheitsgrade der F-Tests (Kontrolle der Typ-I-Fehlerrate)
Wenn Korrekturen zu unterschiedlichen Ergebnissen bzgl. Verwerfung der H0 führen - ggf. Bildung eines Mittelwerts der jeweiligen p-Werte (Field, 2009, S. 476f.)

(Mixed ANOVA wie alle ANOVAs robustes Verfahren)
Sphärizität generell wichtige Voraussetzung - Empfehlung: wenn verletzt, Korrektur notwendig (ansonsten zu hohe Typ-I-Fehlerrate)
Wenn Sphärizität nicht gegeben ist, dann kann man auch eine MANOVA (multivariate ANOVA) berechnen. (wird von SPSS automatisch ausgegeben)

... Greenhouse-Geisser- und Huynh-Feldt-Korrekturen: Bestimmung eines Faktors Epsilon zur Korrektur der Freiheitsgrade der F-Tests (Kontrolle der Typ-I-Fehlerrate)
- Greenhouse-Geisser konservativer (sicherere Variante)
- Huynh-Feldt progressiver
Wenn Korrekturen zu unterschiedlichen Ergebnissen bzgl. Verwerfung der H0 führen - ggf. Bildung eines Mittelwerts der jeweiligen p-Werte (Field, 2009, S. 476f.)

(Mixed ANOVA wie alle ANOVAs robustes Verfahren)
Sphärizität generell wichtige Voraussetzung - Empfehlung: wenn verletzt, Korrektur notwendig (ansonsten zu hohe Typ-I-Fehlerrate)
Wenn Sphärizität nicht gegeben ist, dann kann man auch eine MANOVA (multivariate ANOVA) berechnen. (wird von SPSS automatisch ausgegeben)
- Dafür darf der Box-M-Test nicht signifikant sein um die MANOVA durchzuführen: Varianz-Kovarianz-Matrizen müssen über die unabhängigen Gruppen gleich sein (p > .05)
- Nachteil: MANOVA hat im Allgemeinen eine geringere Testmacht als die mixed design ANOVA

Tags: ANOVA, MANOVA, mixed ANOVA, Sphärizität
Source: VO04
Source: VO04
Was ist die ANCOVA?
Wie im Fall korrelativer Analysen (partielle Korrelation), kann auch im Fall der ANOVA für Dritt(Stör-)variablen kontrolliert werden
.... Kovarianzanalyse (analysis of covariance = ANCOVA)
= Varianzanalyse über die Residuen nach Entfernung des Einflusses der Störvariable auf die abhängige Variable
Ziel: Bereinigung der Daten von Störvariablen - Verkleinerung der Fehlervarianz - Erhöhung der Testmacht
Kovarianzanalyse
ANCOVA vergleicht dann die Messwerte zwischen den Gruppen zum 2. Zeitpunkt (Endpunkt) unter Berücksichtigung der 1. Messung (Baseline) als Kovariate
- Hat mehr Testmacht als mixed design ANOVA
.... Kovarianzanalyse (analysis of covariance = ANCOVA)
= Varianzanalyse über die Residuen nach Entfernung des Einflusses der Störvariable auf die abhängige Variable
Ziel: Bereinigung der Daten von Störvariablen - Verkleinerung der Fehlervarianz - Erhöhung der Testmacht
Kovarianzanalyse
- Abhängige Variable wird auf die Störvariable regrediert. Alles was nicht durch die Störvariable vorhergesagt wird, wird mittels der Varianzanalyse betrachtet (Varianzanalyse auf Residuen)
- Störvariable – nicht gemessen / wenn gemessen wird diese Kontrollvariable genannt
ANCOVA vergleicht dann die Messwerte zwischen den Gruppen zum 2. Zeitpunkt (Endpunkt) unter Berücksichtigung der 1. Messung (Baseline) als Kovariate
- Hat mehr Testmacht als mixed design ANOVA
Tags: ANCOVA
Source: VO04
Source: VO04
Was versteht man unter Stör- und Kontrollvariable?
- Störvariable = Merkmal, das nicht miterhoben (= kontrolliert) wurde, aber die abhängige Variable (potentiell) beeinflusst
- Kontrollvariable = Störvariable, die gemessen (miterhoben) wurde und die nun im Rahmen der Analyse kontrolliert werden kann
Notwendig für die Kovarianzanalyse (analysis of covariance = ANCOVA) = Varianzanalyse über die Residuen nach Entfernung des Einflusses der Störvariable auf die abhängige Variable
Ziel: Bereinigung der Daten von Störvariablen Verkleinerung der Fehlervarianz Erhöhung der Testmacht
Tags: ANCOVA, Kontrollvariable, Störvariable
Source: VO04
Source: VO04
Welche Methode ist statt der mixed ANOVA für diese Untersuchung besser einsetzbar?
Wirkung von CBT (Verhaltenstherapie) im Vergleich zu CBT + Antidepressivum in Depressionsbehandlung

Wirkung von CBT (Verhaltenstherapie) im Vergleich zu CBT + Antidepressivum in Depressionsbehandlung

Für die Auswertung von RCTs mit zwei Messzeitpunkten und 2 oder mehr Gruppen wird allgemein ANCOVA empfohlen (vgl. Van Breukelen, 2006)
In unserem Beispiel sollte eigentlich nicht die mixed design ANOVA verwendet werden, sondern ANCOVA, da diese mehr Testmacht hat.
- ANCOVA vergleicht dann die Messwerte zwischen den Gruppen zum 2. Zeitpunkt (Endpunkt) unter Berücksichtigung der 1. Messung (Baseline) als Kovariate
- Hat mehr Testmacht als mixed design ANOVA
In unserem Beispiel sollte eigentlich nicht die mixed design ANOVA verwendet werden, sondern ANCOVA, da diese mehr Testmacht hat.
Tags: ANCOVA, mixed ANOVA
Source: VO04
Source: VO04
Was kennzeichnet varianzanalytische Methoden im Allgemeinen? Welche Erweiterungen des ALM gibt es?
Varianzanalytische Designs zählen zu den wichtigsten Auswertungsmethoden der gesamten Statistik
- Erlauben die Untersuchung vielfältiger Fragestellungen
- Hohe Flexibilität in der Anwendung
- Allgemeines lineares Modell (ALM) hat jedoch Einschränkungen (Verteilungsannahmen, Homoskedastizität, Linearität, …)
- Erweiterungen des allgemeinen linearen Modells (ALM): - Generalized Linear Model (GLM[GenLin]: Verteilung der abhängigen Variable kann anders als normal sein; Linearität der UV nicht zwingend notwendig)- Generalized Linear Mixed Model (GLMM/GEE: Erweiterung fester Effekte um zufällige; Modellierung unterschiedlichster abhängiger Datenstrukturen (z.B. Verletzung der Sphärizität möglich))
Tags: ALM, Varianzanalyse
Source: VO04
Source: VO04
Wofür sind 4-Felder-Tafeln sinnvoll?
- Kontingenztafeln (4-Felder-Tafeln) dienen der Analyse von Häufigkeiten (count data)
- Analyse von Kontingenztafeln dient der Erfassung von Zusammenhängen – monotoner Zusammenhang (ordinalskalierte Merkmale)– atoner Zusammenhang (nominalskalierte Merkmale): Zusammenhänge haben keine Richtung
In VO Einführung in quantitative Methoden lern(t)en Sie die χ2-basierte Analyse von Kontingenztafeln und den Phi-Korrelationskoeffizient bereits kennen.
Wir beschäftigen uns mit der Einführung und Vertiefung zu (weiteren) v. a. auch klinisch häufig verwendeten Kennwerten von 4-Felder-Tafeln.
Tags: 4-Felder-Tafel
Source: VO05
Source: VO05
Wofür dient die  -basierte Analyse der 4-Felder-Tafeln?
-basierte Analyse der 4-Felder-Tafeln?
 -basierte Analyse der 4-Felder-Tafeln?
-basierte Analyse der 4-Felder-Tafeln? -Test vergleicht beobachtete Häufigkeiten mit erwarteten (bei Zutreffen der H0: „Die beiden Merkmale sind voneinander unabhängig“)
-Test vergleicht beobachtete Häufigkeiten mit erwarteten (bei Zutreffen der H0: „Die beiden Merkmale sind voneinander unabhängig“)Erwartete Häufigkeiten eij ergeben sich aus den Randverteilungen unter Verwendung des Multiplikationstheorems (unabhängige Ereignisse)


(Die erste Formel zeigt, dass jeder Wert mit dem erwarteten Wert verglichen wird. / Die 2. Zeile zeigt die eigentlich, verkürzte Formel.)
- Teststatistik folgt asymptotisch einer
 -Verteilung mit einem Freiheitsgrad (df = 1; allgemein: df = [#Spalten − 1] × [# Zeilen − 1])
-Verteilung mit einem Freiheitsgrad (df = 1; allgemein: df = [#Spalten − 1] × [# Zeilen − 1]) - Test wird einseitig durchgeführt, ist aber i. A. mit ungerichteter Alternativhypothese verbunden (nur große Abweichungen der beobachteten von den erwarteten Werten sprechen für die Alternativhypothese; vgl. ANOVA)
- Kritischer
 -Wert (ungerichtete Hypothese, α = 0.05, df = 1) = 3.84
-Wert (ungerichtete Hypothese, α = 0.05, df = 1) = 3.84
Tags: 4-Felder-Tafel, x2-Test
Source: VO05
Source: VO05
Was sind die Voraussetzungen des  -Tests? Inwiefern ist dies nur eine Approximation?
-Tests? Inwiefern ist dies nur eine Approximation?
 -Tests? Inwiefern ist dies nur eine Approximation?
-Tests? Inwiefern ist dies nur eine Approximation?Voraussetzungen:
 -Test ist ein nicht-parametrischer Test (Daten müssen z.B. nicht normalverteilt sein)
-Test ist ein nicht-parametrischer Test (Daten müssen z.B. nicht normalverteilt sein)
Allerdings: Berechnungsformel (zurückgehend auf Karl Pearson) basiert auf der Approximation der eigentlichen Testverteilung (hypergeometrische Verteilung) durch die Normalverteilung
(zur Erinnerung: das Quadrat einer standardnormalverteilten Variable z ist χ2-verteilt: z2 ~ χ2, mit df = 1)
.... damit Approximation korrekt ist, dürfen erwartete Werte nicht zu klein sein !
Exakter Test durch Fisher-Yates-Test (Fisher‘s exact test).
- Unabhängigkeit (kein Objekt findet sich in mehr als einer Zelle)
- Erwartete Häufigkeiten sind nicht zu klein (alle e > 5) notwendig da dies ein asymptotischer Test/nicht-parametrischer Test ist)
 -Test ist ein nicht-parametrischer Test (Daten müssen z.B. nicht normalverteilt sein)
-Test ist ein nicht-parametrischer Test (Daten müssen z.B. nicht normalverteilt sein)Allerdings: Berechnungsformel (zurückgehend auf Karl Pearson) basiert auf der Approximation der eigentlichen Testverteilung (hypergeometrische Verteilung) durch die Normalverteilung
(zur Erinnerung: das Quadrat einer standardnormalverteilten Variable z ist χ2-verteilt: z2 ~ χ2, mit df = 1)
.... damit Approximation korrekt ist, dürfen erwartete Werte nicht zu klein sein !
Exakter Test durch Fisher-Yates-Test (Fisher‘s exact test).
Tags: 4-Felder-Tafel, x2-Test
Source: VO05
Source: VO05
Welcher Test zum Vergleich der Häufigkeiten der erwarteten Werte liefert exakte Ergebnisse?
Exakter Test durch Fisher-Yates-Test (Fisher‘s exact test)
( -Test hat die Voraussetzung, dass die erwartete Häufigkeiten nicht zu klein sind (alle e > 5) - damit die Approximation korrekt ist)
-Test hat die Voraussetzung, dass die erwartete Häufigkeiten nicht zu klein sind (alle e > 5) - damit die Approximation korrekt ist)
- Verwendet direkt die hypergeometrische Verteilung und basiert auf der Permutation der Zellenhäufigkeiten bei gleichbleibenden Randhäufigkeiten
- Insbesondere für (sehr) kleine Stichproben geeignet !
- Kommt ohne die Voraussetzung e > 5 aus
(
 -Test hat die Voraussetzung, dass die erwartete Häufigkeiten nicht zu klein sind (alle e > 5) - damit die Approximation korrekt ist)
-Test hat die Voraussetzung, dass die erwartete Häufigkeiten nicht zu klein sind (alle e > 5) - damit die Approximation korrekt ist)Tags: 4-Felder-Tafel
Source: VO05
Source: VO05
Was versteht man unter der Kontinuitätskorrektur für die  -basierte Analyse der 4-Felder-Tafel?
-basierte Analyse der 4-Felder-Tafel?
Welche Auswirkungen hat diese?
 -basierte Analyse der 4-Felder-Tafel?
-basierte Analyse der 4-Felder-Tafel?Welche Auswirkungen hat diese?
Kontinuitätskorrektur (Yates-Korrektur):
Häufigkeiten sind diskret, die χ2-Verteilung jedoch stetig - Korrektur der Berechnungsformel

Korrektur erbringt meist jedoch keine grundsätzlich verbesserte
Anpassung an die χ2-Verteilung (vgl. Adler, 1951)
Häufigkeiten sind diskret, die χ2-Verteilung jedoch stetig - Korrektur der Berechnungsformel

Korrektur erbringt meist jedoch keine grundsätzlich verbesserte
Anpassung an die χ2-Verteilung (vgl. Adler, 1951)
- Empfohlen nur, wenn N £ 60
- Führt i. A. zu konservativeren Ergebnissen
Tags: 4-Felder-Tafel, x2-Test
Source: VO05
Source: VO05
Wie kann die Prävalenz eines Merkmals mit der 4-Felder-Tafel überprüft werden und wie kann eine gerichtete Hypothese getestet werden?
Formal kann mittels der Analyse von 4-Felder-Tafeln auch die Differenz von Prozentwerten aus unabhängigen Stichproben überprüft werden
- z.B. Vergleich der Prävalenz eines Merkmals (vorhanden/nicht vorhanden) in unterschiedlichen Stichproben
Anteile (Prozentwerte) können zeilen- und spaltenweise aus 4-Felder- Tafel abgeleitet und darin abgebildet werden:


Ob Prozentwerte unterschiedlich sind, kann mittels χ2-Test geprüft werden
- Hier ist auch Testung einer gerichteten Alternativhypothese möglich
(z.B. H1: „Prävalenz in Stichprobe 1 ist größer als in Stichprobe 2“)
Wie funktioniert Testung gerichteter Hypothese in der Theorie:
Statt kritischen Wert für df = 1 und α = 0.05, jenen für α = 0.10 nehmen (vgl. Bortz, 2005, S. 157)
(in SPSS:
(nur möglich bei 4-Felder-Tafel - zur Erinnerung: das Quadrat einer standardnormalverteilten Variable z ist χ2-verteilt: z2 ~ χ2,
mit df = 1)
- z.B. Vergleich der Prävalenz eines Merkmals (vorhanden/nicht vorhanden) in unterschiedlichen Stichproben
Anteile (Prozentwerte) können zeilen- und spaltenweise aus 4-Felder- Tafel abgeleitet und darin abgebildet werden:


Ob Prozentwerte unterschiedlich sind, kann mittels χ2-Test geprüft werden
- Hier ist auch Testung einer gerichteten Alternativhypothese möglich
(z.B. H1: „Prävalenz in Stichprobe 1 ist größer als in Stichprobe 2“)
Wie funktioniert Testung gerichteter Hypothese in der Theorie:
Statt kritischen Wert für df = 1 und α = 0.05, jenen für α = 0.10 nehmen (vgl. Bortz, 2005, S. 157)
- kritischer χ2-Wert = 2.71 statt 3.84
- mehr Testmacht
(in SPSS:
- p-Wert halbieren,
- α verdoppeln oder
- einseitigen p-Wert des Fisher-Tests heranziehen)
(nur möglich bei 4-Felder-Tafel - zur Erinnerung: das Quadrat einer standardnormalverteilten Variable z ist χ2-verteilt: z2 ~ χ2,
mit df = 1)
- Testung gerichteter Hypothese nur möglich bei df = 1 !!!
- Bei einem Freiheitsgrad ist χ2-Verteilung die Verteilung einer quadrierten standardnormalverteilten Variable: - Symmetrie-Eigenschaften der Normalverteilung können hier eingesetzt werden für einseitige Testungen
Tags: 4-Felder-Tafel, Prävalenz
Source: VO05
Source: VO05
Was sind die Prävalenzen für diese Fragestellung:
Besteht zwischen familiärer Belastung und dem Manifestationsalter juveniler Epilepsie ein Zusammenhang?

Besteht zwischen familiärer Belastung und dem Manifestationsalter juveniler Epilepsie ein Zusammenhang?

Anders formuliert als Unterschiedshypothese:
Ist die Prävalenz familiärer Vorbelastung höher in Fällen mit früherem Beginn?
7-12 Jahre: 5/(5 + 6) = 0.45 45%
13-18 Jahre: 5/(5 + 24) = 0.17 17%
Ist die Prävalenz familiärer Vorbelastung höher in Fällen mit früherem Beginn?
7-12 Jahre: 5/(5 + 6) = 0.45 45%
13-18 Jahre: 5/(5 + 24) = 0.17 17%
Tags: 4-Felder-Tafel, Prävalenz
Source: VO05
Source: VO05
Was zeigt dieser SPSS-Ausdruck?




Ergebnis zu dieser Fragestellung:
Besteht zwischen familiärer Belastung und dem Manifestationsalter juveniler Epilepsie ein Zusammenhang?

Kontinuitätskorrektur ist konservativer (höherer p-Wert). Man muss sich überlegen welchen Test man heranzieht.
In der letzten Zeile steht noch dass nicht in allen Zellen die Häufigkeit größer als 5 sind (ev. Sample zu klein):
Nicht alle e > 5 !
Besteht zwischen familiärer Belastung und dem Manifestationsalter juveniler Epilepsie ein Zusammenhang?

Kontinuitätskorrektur ist konservativer (höherer p-Wert). Man muss sich überlegen welchen Test man heranzieht.
In der letzten Zeile steht noch dass nicht in allen Zellen die Häufigkeit größer als 5 sind (ev. Sample zu klein):
Nicht alle e > 5 !
- exakten Test heranziehen
- kein signifikantes Ergebnis
Tags: 4-Felder-Tafel, Prävalenz
Source: VO05
Source: VO05
Was zeigt dieser SPSS-Ausdruck?


In welcher Zelle ist e < 5 ?
Zeigt welches Sample zu klein ist um die Voraussetzungen für die -basierte Analyse von 4-Felder-Tafeln zu erfüllen.
-basierte Analyse von 4-Felder-Tafeln zu erfüllen.
Man sollte sich an einem exakten Test orientieren.
Zeigt welches Sample zu klein ist um die Voraussetzungen für die
 -basierte Analyse von 4-Felder-Tafeln zu erfüllen.
-basierte Analyse von 4-Felder-Tafeln zu erfüllen.Man sollte sich an einem exakten Test orientieren.
Tags: 4-Felder-Tafel, x2-Test
Source: VO05
Source: VO05
Was ist der Phi-Koeffizient? Welche Eigenschaften hat dieser?
Phi-Koeffizient: Produkt-Moment-Korrelation über zwei dichotome Merkmale

Vorzeichen nur dann von Bedeutung, wenn Merkmale ordinal - (monotoner Zusammenhang)
Wenn es nur nominal skalierte Merkmale sind, so verzichtet man auf ein Vorzeichen (man hat dann nur positive Werte) = atoner Zusammenhang.
rφ hat prinzipiell Eigenschaften eines Korrelationskoeffizienten
(Wertebereich −1 bis +1)
Cave: praktisch ist Wertebereich durch Randverteilungen eingeschränkt - maximaler Zusammenhang |rφ max | < 1 (nur bei gleichen Randverteilungen keine Einschränkungen)

Randverteilung muss gleich sein – damit phi-Koeffizient zw. 0 und 1 liegt. Die Verteilung darf schief sein, jedoch muss sie gleich schief sein.
- Bei einer ungleich schiefen Verteilung wie im 2. Beispiel kann der phi-Koeffizient maximal 0,429 werden. D.h. es gibt kein gutes Kriterium mehr um bei der Interpretation festzulegen ob ein Zusammenhang gut oder weniger gut ist.

Vorzeichen nur dann von Bedeutung, wenn Merkmale ordinal - (monotoner Zusammenhang)
Wenn es nur nominal skalierte Merkmale sind, so verzichtet man auf ein Vorzeichen (man hat dann nur positive Werte) = atoner Zusammenhang.
rφ hat prinzipiell Eigenschaften eines Korrelationskoeffizienten
(Wertebereich −1 bis +1)
Cave: praktisch ist Wertebereich durch Randverteilungen eingeschränkt - maximaler Zusammenhang |rφ max | < 1 (nur bei gleichen Randverteilungen keine Einschränkungen)

Randverteilung muss gleich sein – damit phi-Koeffizient zw. 0 und 1 liegt. Die Verteilung darf schief sein, jedoch muss sie gleich schief sein.
- Bei einer ungleich schiefen Verteilung wie im 2. Beispiel kann der phi-Koeffizient maximal 0,429 werden. D.h. es gibt kein gutes Kriterium mehr um bei der Interpretation festzulegen ob ein Zusammenhang gut oder weniger gut ist.
Tags: 4-Felder-Tafel, phi-Koeffizient
Source: VO05
Source: VO05
Warum kann der Wertebereich des Phi-Koeffizienten eingeschränkt sein? Wie kann dies korrigiert werden?
Cave: praktisch ist Wertebereich durch Randverteilungen eingeschränkt - maximaler Zusammenhang |rφ max | < 1 (nur bei gleichen Randverteilungen keine Einschränkungen)

Randverteilung muss gleich sein – damit phi-Koeffizient zw. 0 und 1 liegt. Die Verteilung darf schief sein, jedoch muss sie gleich schief sein.
- Bei einer ungleich schiefen Verteilung wie im 2. Beispiel kann der phi-Koeffizient maximal 0,429 werden. D.h. es gibt kein gutes Kriterium mehr um bei der Interpretation festzulegen ob ein Zusammenhang gut oder weniger gut ist.
Einschränkung des Wertebereichs kein eigentliches Spezifikum von rφ
//Dies gibt es bei allen Korrelationskoeffizienten - jedoch tritt vor allem bei 4-Felder-Korrelation der Effekt extrem stark auf.
Gilt ebenso für Produkt-Moment-Korrelation metrischer Variablen, wenn diese nicht gleiche Verteilungen aufweisen (Carroll, 1961)

Signifikanztestung von rφ ergibt sich über χ2-Test
... Testmacht des χ2-Tests ebenso bei ungleichen Randverteilungen eingeschränkt

Randverteilung muss gleich sein – damit phi-Koeffizient zw. 0 und 1 liegt. Die Verteilung darf schief sein, jedoch muss sie gleich schief sein.
- Bei einer ungleich schiefen Verteilung wie im 2. Beispiel kann der phi-Koeffizient maximal 0,429 werden. D.h. es gibt kein gutes Kriterium mehr um bei der Interpretation festzulegen ob ein Zusammenhang gut oder weniger gut ist.
Einschränkung des Wertebereichs kein eigentliches Spezifikum von rφ
//Dies gibt es bei allen Korrelationskoeffizienten - jedoch tritt vor allem bei 4-Felder-Korrelation der Effekt extrem stark auf.
Gilt ebenso für Produkt-Moment-Korrelation metrischer Variablen, wenn diese nicht gleiche Verteilungen aufweisen (Carroll, 1961)

- Formeln für rφ max finden sich z.B. in Bortz, Lienert & Böhnke (2008, S. 327ff.)
- Korrektur wird jedoch nicht empfohlen rφ ist Maß des linearen Zusammenhangs kann nur bei gleicher Randverteilung maximal sein
- Korrigiertes rφ kein Maß mehr des (rein) linearen Zusammenhangs
Signifikanztestung von rφ ergibt sich über χ2-Test
... Testmacht des χ2-Tests ebenso bei ungleichen Randverteilungen eingeschränkt
Tags: 4-Felder-Tafel, Phi-Koeffizienz
Source: VO05
Source: VO05
Was zeigt dieser SPSS-Ausdruck?

rφ max = .5
Welche Auswirkung hat hier die Korrektur des Phi-Korrelationskoeffizienten?

rφ max = .5
Welche Auswirkung hat hier die Korrektur des Phi-Korrelationskoeffizienten?
Phi-Korrelationskoeffizient
Für diese Tafel gilt:
rφ max = .5

rφ* = .291/.5 = .582
Korrigiertes rφ doppelt so hoch wie nicht-korrigiertes!
Wir würden den Zusammenhang zur Hälfte unterschätzen, wenn man nur die 4-Felder-Tafel berücksichtigt.
(Stattdessen kann z.b. das odds-ratio verwendet werden)
Für diese Tafel gilt:
rφ max = .5

rφ* = .291/.5 = .582
Korrigiertes rφ doppelt so hoch wie nicht-korrigiertes!
Wir würden den Zusammenhang zur Hälfte unterschätzen, wenn man nur die 4-Felder-Tafel berücksichtigt.
(Stattdessen kann z.b. das odds-ratio verwendet werden)
Tags: phi-Korrelationskoeffizient, x2-Test
Source: VO05
Source: VO05
Was ist das odds-ratio und welche Eigenschaften hat dieser Wert?
Odds Ratio: OR; Chancenverhältnis, Quotenverhältnis, Kreuzproduktquotient
Chance ≠ Wahrscheinlichkeit
Wahrscheinlich a = a/(a+b)
Chance a:b (a wird direkt mit b verglichen ohne Bezug auf eine Grundgesamtheit)

a/b und c/d bezeichnen Chancen (z.B. 1:3) - OR ist Verhältnis dieser Chancen
(Wie hoch ist die Chance a/b zu beobachten im Verhältnis zu c/d?)
Symmetrisch bedeutet, dass X und Y vertauscht werden können, OR bleibt aber ident

 ebenso ein symmetrisches Maß, Risk Ratio (siehe später) aber nicht
ebenso ein symmetrisches Maß, Risk Ratio (siehe später) aber nicht
Weitere Eigenschaft: werden Zeilen oder Spalten vertauscht, wird der Kehrwert (= OR‘) des OR bestimmt

Chance ≠ Wahrscheinlichkeit
Wahrscheinlich a = a/(a+b)
Chance a:b (a wird direkt mit b verglichen ohne Bezug auf eine Grundgesamtheit)
- insbesondere in klinischer Forschung vielverwendet
- Generell für etliche statistische Tests und Methoden von Bedeutung (z.B. logistische Regression)
- OR ist ein symmetrisches Maß des Zusammenhangs für 4-Felder-Tafeln

a/b und c/d bezeichnen Chancen (z.B. 1:3) - OR ist Verhältnis dieser Chancen
(Wie hoch ist die Chance a/b zu beobachten im Verhältnis zu c/d?)
Symmetrisch bedeutet, dass X und Y vertauscht werden können, OR bleibt aber ident

 ebenso ein symmetrisches Maß, Risk Ratio (siehe später) aber nicht
ebenso ein symmetrisches Maß, Risk Ratio (siehe später) aber nichtWeitere Eigenschaft: werden Zeilen oder Spalten vertauscht, wird der Kehrwert (= OR‘) des OR bestimmt

Tags: odds ratio
Source: VO05
Source: VO05
Welchen Wertebereich kann das odds ratio annehmen?
OR hat einen Wertebereich von 0 bis unendlich, kann nur positiv sein
Interpretation
ORs werden auch logarithmiert verwendet log OR (natürlicher Logarithmus) Wertebereich -∞ und +∞, log OR = 0 kein Zusammenhang
Beispiel

Interpretation
- OR = 1: kein Zusammenhang vorhanden, Chancen sind gleichgroß, unterscheiden sich nicht (a/b = c/d)
- OR > 1: in Gruppe x = 1 sind die Chancen für y = 1 größer als in Gruppe x = 0 (a/b > c/d)
- OR < 1: in Gruppe x = 1 sind die Chancen für y = 1 kleiner als in Gruppe x = 0 (a/b < c/d)
ORs werden auch logarithmiert verwendet log OR (natürlicher Logarithmus) Wertebereich -∞ und +∞, log OR = 0 kein Zusammenhang
Beispiel

- Chancen einer frühen Manifestation bei familiärer Belastung 5:5 (oder 1:1)
- Chancen einer frühen Manifestation bei keiner Belastung 6:24
- Chancen bei familiärer Belastung 4-fach erhöht:

Tags: 4-Felder-Tafel, odds ratio
Source: VO05
Source: VO05

Was ist die Chance
a) einer frühen Manifestation bei familiärer Belastung?
b) einer frühen Manifestation bei keiner Belastung?
c) bei familiärer Belastung?

a)
Chancen einer frühen Manifestation bei familiärer Belastung 5:5 (oder 1:1)
b) Chancen einer frühen Manifestation bei keiner Belastung 6:24
c) Chancen bei familiärer Belastung 4-fach erhöht:

Tags: 4-Felder-Tafel, odds ratio
Source: VO05
Source: VO05
Was zeigt dieser SPSS Ausdruck?


Odds-ratio für folgendes Beispiel inkl. Konfidenzintervall:

Zeigt das Odds ratio mit 4 an: Chancen bei familiärer Belastung 4-fach erhöht

Konfidenzintervall des OR inkludiert auch den Wert 1 (1=kein Zusammenhang vorhanden, Chancen sind gleichgroß)
- kein signifikant erhöhtes Quotenverhältnis;
Test der Signifikanz kann i. A. auch über χ2-Test erfolgen

Zeigt das Odds ratio mit 4 an: Chancen bei familiärer Belastung 4-fach erhöht

Konfidenzintervall des OR inkludiert auch den Wert 1 (1=kein Zusammenhang vorhanden, Chancen sind gleichgroß)
- kein signifikant erhöhtes Quotenverhältnis;
Test der Signifikanz kann i. A. auch über χ2-Test erfolgen
Tags: 4-Felder-Tafel, Konfidenzintervall, odds ratio
Source: VO05
Source: VO05
Was ist das Maß des "realtiven Risikos" (risk ratio)? Was sind die Eigenschaften und wann kann dieser verwendet werden?
Relatives Risiko (RR; relative risk, risk ratio) wie Odds Ratio wichtiger Kennwert in klinischer Forschung
RR gibt Auskunft darüber, ob das Vorhandensein eines (Risiko-) Faktors die Wahrscheinlichkeit (!= Chancen !!!) für ein bestimmtes (erwünschtes oder unerwünschtes) Outcome erhöht oder erniedrigt

Typische Fragestellungen für Anwendung des RR:
RR gibt Auskunft darüber, ob das Vorhandensein eines (Risiko-) Faktors die Wahrscheinlichkeit (!= Chancen !!!) für ein bestimmtes (erwünschtes oder unerwünschtes) Outcome erhöht oder erniedrigt

- RR hat nicht die vielen rechnerischen günstigen Eigenschaften des OR
- Ist nicht symmetrisch und Vertauschen von Zeilen oder Spalten führt nicht zur Berechnung des Kehrwerts des Koeffizienten
- Inhaltlich macht Anwendung des RR zudem nur in longitudinalen Studiendesigns (Längsschnittstudien) Sinn: – Kohortenstudien und– RCTs
- Fragestellungen zur Inzidenz (Auftreten eines definierten Ereignisses während eines definierten Beobachtungszeitraums) - Der Risikofaktor liegt bei den Vpn von Anfang an vor
- In bloßen Querschnittsstudien (Fall-Kontroll-Studien, Ein-Punkt-Erhebungen bzw. retrospektive Studien) ist Inzidenz nicht erhebbar.
Typische Fragestellungen für Anwendung des RR:
- Longitudinale Studien zum Auftreten (Inzidenz) von Erkrankungen in Abhängigkeit vom Vorhandensein definierter Risikofaktoren
- Vergleich zweier Behandlungsmethoden (clinical trial)
Tags: 4-Felder-Tafel, risk ratio
Source: VO05
Source: VO05
Was sind typische Fragestellungen zur Anwendung des Risk Ratio (relatives Risiko)?
Typische Fragestellungen für Anwendung des RR:
(In nicht longitudinalen Studien darf kein RR erhoben werden, da man keinen Zeitverlauf hat)
- Longitudinale Studien zum Auftreten (Inzidenz) von Erkrankungen in Abhängigkeit vom Vorhandensein definierter Risikofaktoren
- Vergleich zweier Behandlungsmethoden (clinical trial)
(In nicht longitudinalen Studien darf kein RR erhoben werden, da man keinen Zeitverlauf hat)
Tags: risk ratio
Source: VO06
Source: VO06
Was ist der Wertebereich des risk ratio?
RR hat einen Wertebereich von 0 bis unendlich, kann nur positiv sein
- RR = 1: keine Änderung der Inzidenz des definierten Outcomes durch Risikofaktor P(Krankheit+|Risiko+) = P(Krankheit+|Risiko−)(Kein Zusammenhang)
- RR > 1: Risikofaktor erhöht Inzidenz des definierten Outcomes P(Krankheit+|Risiko+) > P(Krankheit+|Risiko−)(Unterschied zwischen 2 Gruppen - Vorhandensein des Risikofaktors erhöht die Inzidenz der Krankheit)
- RR < 1: Risikofaktor erniedrigt Inzidenz des definierten Outcomes P(Krankheit+|Risiko+) < P(Krankheit+|Risiko−)(Hier spricht man dann nicht von Risikofaktoren, sondern von protektiven Faktoren)
Tags: risk ratio
Source: VO06
Source: VO06
Inwiefern sind odds ratio und risk ratio miteinander verwandt?
für seltene Ereignisse ist OR ein approximativer Schätzer des RR

(also kann man den RR schätzen obwohl man keinen longitudinale Studie hat - wird manchmal in der angewandten Forschung verwendet)
(OR = Chance // Risk ratio = Auftrittswahrscheinlichkeit)

(also kann man den RR schätzen obwohl man keinen longitudinale Studie hat - wird manchmal in der angewandten Forschung verwendet)
(OR = Chance // Risk ratio = Auftrittswahrscheinlichkeit)
Tags: odds ratio, risk ratio
Source: VO06
Source: VO06
Wie unterscheiden sich risk ratio und odds ratio?
- In der Interpretation sind OR und RR grundverschieden
- OR erlaubt Aussagen dazu, ob Chancen eines Ereignisses/Merkmals durch ein anderes Ereignis/Merkmal erhöht oder erniedrigt werden
- RR erlaubt Aussagen dazu, ob die Auftrittswahrscheinlichkeit eines Ereignisses/Merkmals (Outcome) durch ein anderes Ereignis/Merkmal (Risiko) erhöht wird
- Chance != Auftrittswahrscheinlichkeit
- OR und RR bezeichnen in beiden Fällen jedoch ein Verhältnis: Chancen oder Wahrscheinlichkeit wird um ein x-faches erhöht oder erniedrigt
Tags: odds ratio, risk ratio
Source: VO06
Source: VO06
Beispiel:

Sind die Remissionsraten signifikant?
Was ist das RR?




Sind die Remissionsraten signifikant?
Was ist das RR?



Siehe Chi-Quadrat-Tests:
Risikoschätzer
- Unterschied der Remissionsraten signifikant;
- gerichtete Hypothese (p könnte noch halbiert werden)
Risikoschätzer
- Zwei Zahlenangaben zum RR;
- „Kohorten-Analyse Remission = remittiert“: bezieht sich auf RR, das uns interessiert - Remissionsrate um das 2.7-fache gesteigert
- „Kohorten-Analyse Remission = nicht remittiert“ berechnet d.h. die Wahrscheinlichkeit, nicht zu remittieren, wird durch die gleichzeitige Gabe von Antidepressiva um fast die Hälfte gesenkt
- Achtung: 0.584 ist nicht Kehrwert von 2.701 !!! (1/2.701 = 0.370)
- Kodierung der Variablen (aufsteigend von links nach rechts in Spalten, aufsteigend von oben nach unten in Zeilen) und Setzen der richtigen Variable in die Spalten der 4-Felder-Tafel in SPSS entscheidend, welches RR berechnet wird
Tags: risk ratio, SPSS
Source: VO06
Source: VO06
Was versteht man unter Sensitivität und Spezifität? Was ist ein häufiger Anwendungsfall?
- Sensitivität und Spezifität weitere Kennwerte, die sich in 4-Felder-Tafeln darstellen und aus 4-Felder-Tafeln folgern lassen
- Wichtig für diagnostische Tests: Medizin, (klinische) Psychologie, etc.
- Sensitivität = Wahrscheinlichkeit, dass Test einen positiven Fall erkennt - bedingte Wahrscheinlichkeit: P(Test +|Krankheit +) (Krankheit liegt vor und der Test erkennt es)
- Spezifität = Wahrscheinlichkeit, dass Test einen negativen Fall erkennt bedingte Wahrscheinlichkeit: P(Test −|Krankheit −) (Krankheit liegt nicht vor und der Test sagt dass die Antwort nicht vor liegt)
- Stehen im Zusammenhang mit Typ-I- (falsch-positive Fälle) und Typ-II Fehlerraten (falsch-negative Fälle) diagnostischer Tests
- Für Erhebung von Sensitivität und Spezifität, muss wahrer Status (Krankheit + oder −) bekannt sein Vergleich mit Gold Standard (Man muss wissen ob eine Krankheit vorliegt oder nicht - z.B. durch etabliertes, aufwändiges Verfahren)
- Häufiger Anwendungsfall: Erhebung der Güte eines Screenings gegenüber einem längeren, aufwändigeren etablierten Verfahren

Sensitivität und Spezifität wichtige Kennwerte eines diagnostischen Tests je nach Anwendungsfall wichtig, ob eine hohe Sensitivität oder eine hohe Spezifität gegeben sein sollte
Tags: 4-Felder-Tafel, Sensitivität, Spezifität
Source: VO06
Source: VO06
Wie werden folgende Werte berechnet?
- Sensitivität
- Spezifität
- Falsch-positive Fälle
- Falsch negative Fälle

- Sensitivität
- Spezifität
- Falsch-positive Fälle
- Falsch negative Fälle



Tags: 4-Felder-Tafel, Sensitivität, Spezifität
Source: VO06
Source: VO06
Inwiefern hängt Sensitivität/Spezifität ab von der Prävalenz einer Krankheit?
Inwiefern hängt NPV/PPV von der Prävalenz ab?
Inwiefern hängt NPV/PPV von der Prävalenz ab?
Sensitivität und Spezifität sind nicht von Prävalenz der Erkrankung abhängig - es ist eine Eigenschaften des Tests
PPV (positiver Vorhersagewert) und NPV (negative Vorhersagewert) sind stark prävalenzabhängig.
PPV (positiver Vorhersagewert) und NPV (negative Vorhersagewert) sind stark prävalenzabhängig.
- D.h. ob man der Aussage eines Tests trauen kann (Zuverlässigkeit), hängt nicht nur von Sensitivität und Spezifität ab, sondern auch von der Prävalenz des untersuchten Merkmals
Tags: NPV, PPV, Prävalenz, Sensitivität, Spezifität
Source: VO06
Source: VO06
Was bedeutet wenn ein Testverfahren eine hohe Sensitivität aufweist?
- Vorliegen der Erkrankung wird mit hoher Wahrscheinlichkeit erkannt
- übertrieben gesagt für 100%: alle, die Krankheit haben, sind auch im Test auffällig
- negatives Testergebnis starker Hinweis, dass Erkrankung nicht vorliegt
Tags: Sensitivität
Source: VO06
Source: VO06
Was bedeutet wenn ein Testverfahren eine hohe Spezifität aufweist?
- Fehlen der Erkrankung wird mit hoher Wahrscheinlichkeit erkannt
- übertrieben gesagt für 100%: alle, die Krankheit nicht haben, sind auch im Test unauffällig
- positives Testergebnis starker Hinweis, dass Erkrankung vorliegt
Tags: Spezifität
Source: VO06
Source: VO06
Was ist der positive Vorhersagewert bzw. negative Vorhersagewert?
Wie wahrscheinlich ist es, dass ein positives Testergebnis auf ein tatsächlich vorliegende Krankheit hinweist.
In der Anwendung (klinische Diagnostik) ist man an der bedingten Wahrscheinlichkeit interessiert, dass die Krankheit vorliegt, wenn der Test positiv ausfällt

PPV und NPV stark prävalenzabhängig.
In der Anwendung (klinische Diagnostik) ist man an der bedingten Wahrscheinlichkeit interessiert, dass die Krankheit vorliegt, wenn der Test positiv ausfällt

PPV und NPV stark prävalenzabhängig.
- D.h. ob man der Aussage eines Tests trauen kann (Zuverlässigkeit), hängt nicht nur von Sensitivität und Spezifität ab, sondern auch von der Prävalenz des untersuchten Merkmals
Tags: NPV, PPV, Prävalenz
Source: VO06
Source: VO06
Was sind die Werte für:
- Sensitivität
- Spezifität
- Falsch-positive Werte
- Falsch-negative Werte
- PPV
- NPV

Wie verändern sich die Werte, wenn die Prävalenz 10x so hoch ist (Z.B. in einer Risikogruppe)?
- Sensitivität
- Spezifität
- Falsch-positive Werte
- Falsch-negative Werte
- PPV
- NPV

Wie verändern sich die Werte, wenn die Prävalenz 10x so hoch ist (Z.B. in einer Risikogruppe)?


Wenn Prävalenz niedrig:
- negatives Ergebnis sehr zuverlässiger Indikator, dass Krankheit −;
- positives Testergebnis allerdings schlechter Indikator, dass Krankheit +

(Anmerkung: bei der Prüfung muss nichts berechnet werden)
Tags: NPV, PPV, Prävalenz, Sensitivität, Spezifität
Source: VO06
Source: VO06
Wie können die Werte zu Sensitivität, Spezifität, PPV und NPV interpretiert werden?
Man kann alle diese Variablen berechnen, aber interferenzstatistische Aussagekraft ist unklar.
- Alle Maßzahlen deskriptive Maße
- Interpretation (inferenzstatische Absicherung) kann durch signifikanten χ2-Wert der Vierfeldertalfel erfolgen
- Ebenso es möglich, Konfidenzintervalle zu bestimmen (wird aber nicht von SPSS zur Verfügung gestellt)
- Wichtige Take-Home-Message zu PPV/NPV: Interpretation der Ergebnisse diagnostischer Tests (Liegt Krankheit vor oder nicht?) ist abhängig von Prävalenzraten
Tags: NPV, PPV, Sensitivität, Spezifität
Source: VO06
Source: VO06
Warum ist die Betrachtung von Effektstärken sinnvoll? Wo werden diese eingesetzt?
- Nicht nur statistische Signifikanz für Bedeutsamkeit eines Ergebnisses ausschlaggebend
- Größe und Richtung eines Effektes (z.B. Mittelwertsunterschied, Zusammenhang) inhaltlich relevant
- APA (American Psychological Association) empfiehlt das Berichten von Effektgrößen zusätzlich zu den Ergebnissen statistischer Tests - Veranschaulichung der inhaltlichen Bedeutsamkeit eines Ergebnisses
- Im Bereich der klinischen und medizinischen Forschung sind Effektgrößen unmittelbar wichtig (Wie gut wirkt eine Behandlung? Wie groß ist der Einfluss eines Risikofaktors?)
- Effektgrößen nicht nur für Veranschaulichung von Ergebnissen wichtig
- Ebenso für Planung von Studien relevant: – Effektgröße– Alpha-Fehler– Beta-Fehler– Stichprobengrößestehen miteinander in Beziehung
- Kennt man drei der vier Parameter (oder legt sie a priori fest) kann der vierte berechnet werden - Planung von Stichprobengrößen, Ermittlung der Power einer Studie
Tags: Effektgröße
Source: VO06
Source: VO06
Welche 2 Arten von Effektgrößen können unterschieden werden? Was sind Maße für diese Effektgrößen?
Standardisierte und unstandardisierte Effektgrößen
Unstandardisierte Effektgrößen sind Maße, die eine unmittelbare inhaltliche Bedeutsamkeit und Interpretation haben, z.B.
Maße für unstandardisierte Effektgrößen z.B.
Standardisierte Effektgrößen i. A. vor allem dann von Bedeutung, wenn zugrundeliegendes Maß keine unmittelbare Interpretation gestattet, z.B. Summenwerte in psychologischen Tests und Fragebögen
Standardisierte Effektgrößen erlauben Vergleich von Ergebnissen mit Instrumenten, die unterschiedliche Skalierung haben - Unterschiede werden durch Standardisierung kompensiert
Anwendung von Effektmaßen (standardisiert, unstandardisiert) vor allem auch in meta-analytischer Forschung (= Integration von Forschungsergebnissen unterschiedlicher Studien zur selben Forschungsfrage)
Häufig verwendete standardisierte Maße
Unstandardisierte Effektgrößen sind Maße, die eine unmittelbare inhaltliche Bedeutsamkeit und Interpretation haben, z.B.
- Anzahl an Zigaretten, die im Schnitt pro Tag geraucht werden
- Krankenstandstage pro Jahr, die durchschnittlich auf einer bestimmte Erkrankung zurückgeführt werden können
- Gewichtsverlust in kg, der durch ein bestimmtes Diäts- und Aktivitätsprogramm im Schnitt erzielt werden kann
Maße für unstandardisierte Effektgrößen z.B.
- Differenz von Gruppenmittelwerten (raw mean difference)
- Unstandardisierte Regressionskoeffizienten
Standardisierte Effektgrößen i. A. vor allem dann von Bedeutung, wenn zugrundeliegendes Maß keine unmittelbare Interpretation gestattet, z.B. Summenwerte in psychologischen Tests und Fragebögen
- Summenwert u. a. abhängig von Anzahl der Items und Anzahl der Abstufungen, die zur Beantwortung eines Items vorhanden sind
- Zwei Instrumente, die dasselbe gleich gut erfassen, haben durch Unterschiede in Itemanzahl und Itemabstufungen Unterschiede in ihrer Skalierung
- Skalierungsunterschiede sind artifiziell; sagen nichts über Unterschiede in der eigentlich gemessenen Eigenschaft aus
Standardisierte Effektgrößen erlauben Vergleich von Ergebnissen mit Instrumenten, die unterschiedliche Skalierung haben - Unterschiede werden durch Standardisierung kompensiert
Anwendung von Effektmaßen (standardisiert, unstandardisiert) vor allem auch in meta-analytischer Forschung (= Integration von Forschungsergebnissen unterschiedlicher Studien zur selben Forschungsfrage)
Häufig verwendete standardisierte Maße
- Cohens d (und andere Maße der d-Familie)
- Produkt-Moment-Korrelation r (und andere Maße der r-Familie)
- Eta2 (und andere Maße der Varianzaufklärung)
- Odds Ratio und Risk Ratio (und davon abgeleitete Kennwerte)
Tags: Effektgröße
Source: VO06
Source: VO06
Was misst das Cohens d?
Standardisierte Effektgröße

Cohens d gibt den Abstand zweier Verteilungen in Einheiten ihrer
gemeinsamen Standardabweichung an

Annahmen: Normalverteilung, Homogenität der Varianzen (t-Test !!!)
- Cohens d relevant für alle Mittelwertsvergleiche zwischen zwei (unabhängigen oder abhängigen) Gruppen
- Kann aus Gruppenmittelwerten, Standardabweichungen und ns oder aus der t-Statistik des t-Test berechnet werden (wird nicht von SPSS ausgegeben)

Cohens d gibt den Abstand zweier Verteilungen in Einheiten ihrer
gemeinsamen Standardabweichung an

Annahmen: Normalverteilung, Homogenität der Varianzen (t-Test !!!)
Tags: Cohens d, Effektgröße
Source: VO06
Source: VO06
Was sind die Annahmen für Cohens d?
Wie wird Cohens d für abhängige bzw. unabhängige Stichproben berechnet?
Wie wird Cohens d für abhängige bzw. unabhängige Stichproben berechnet?
Annahmen: Normalverteilung, Homogenität der Varianzen (t-Test !!!)
Cohens d gibt den Abstand zweier Verteilungen in Einheiten ihrer
gemeinsamen Standardabweichung an



Cohens d gibt den Abstand zweier Verteilungen in Einheiten ihrer
gemeinsamen Standardabweichung an



Tags: Cohens d, Effektgröße
Source: VO06
Source: VO06
Wann spricht man bei Cohens d von einem kleinen, mittleren oder großen Effekt?
Faustregeln und Richtlinien zur Einschätzung der Größe eines Effekts (Cohen, 1988)


Tags: Cohens d, Effektgröße
Source: VO06
Source: VO06
Wie erfolgt die Berechnung des Cohens d für folgendes Beispiel - Welche Berechnungsschritte sind notwendig?

- Was bedeutet ein Ergebnis vom Cohens d von 1.83?

- Was bedeutet ein Ergebnis vom Cohens d von 1.83?
Standardabweichung wird auf das gleiche Maß gebracht und diese werden dann verglichen.
Analyse (t-Test für abhängige Daten) hat gezeigt, dass Veränderung hochsignifikant war – Größe des Effekts?
- Unserer Effekt war signifikant – aber wie groß ist denn der Effekt?
- Korrelation von 0,66 – Pre- und Post-Testwerte
- T-Wert und N wird zur Berechnung noch benötigt.


Dann muss die Berechnung des Cohens d manuell durchgeführt werden (in SPSS ist das Cohens d nicht implementiert.)


1,83 – sehr großer Effekt / auch 1,51 ist noch ein sehr großer Effekt.
Um keine Über – oder Unterschätzungen von Effekten zu haben, sollte die Formel mit den unabhängigen Designs verwendet werden.
Analyse (t-Test für abhängige Daten) hat gezeigt, dass Veränderung hochsignifikant war – Größe des Effekts?
- Unserer Effekt war signifikant – aber wie groß ist denn der Effekt?
- Korrelation von 0,66 – Pre- und Post-Testwerte
- T-Wert und N wird zur Berechnung noch benötigt.


Dann muss die Berechnung des Cohens d manuell durchgeführt werden (in SPSS ist das Cohens d nicht implementiert.)


1,83 – sehr großer Effekt / auch 1,51 ist noch ein sehr großer Effekt.
Um keine Über – oder Unterschätzungen von Effekten zu haben, sollte die Formel mit den unabhängigen Designs verwendet werden.
Tags: Cohens d, Effektgröße
Source: VO06
Source: VO06
Welchen Einfluss hat r auf die Berechnung des Cohens d?
Wenn r > .5, ist d der Differenzwerte größer als d in Metrik unabhängiger Stichproben (bei r = .5 idente Ergebnisse; ansonsten kleiner)
Beispiel:

In Messwiederholungsdesigns sollte d in der Metrik unabhängiger Stichproben berechnet werden (vgl. Dunlap et al., 1996) ansonsten droht Über- oder Unterschätzung von Effekten und Vergleiche mit Untersuchungen mit unabhängigen Designs (VG vs. KG) werden erschwert
Beispiel:

In Messwiederholungsdesigns sollte d in der Metrik unabhängiger Stichproben berechnet werden (vgl. Dunlap et al., 1996) ansonsten droht Über- oder Unterschätzung von Effekten und Vergleiche mit Untersuchungen mit unabhängigen Designs (VG vs. KG) werden erschwert
Tags: Cohens d, Effektgröße
Source: VO06
Source: VO06
Welche anderen Indizes werden ähnlich berechnet wie Cohens d?
Neben Cohens d existieren noch weitere verwandte Indizes, die ähnlich berechnet werden: z.B. Hedges g, Glass Δ.
- Cohens d vermutlich am meisten verwendet
- Cohens d vermutlich am meisten verwendet
Tags: Cohens d, Effektgröße
Source: VO06
Source: VO06
Was ist das Effektmaß Produkt-Moment-Korrelation r? Was sind Anforderungen an die Daten?
- Produkt-Moment-Korrelation r ist bereits selbst ein standardisiertes Effektmaß
- Wertebereich auf −1 bis +1 beschränkt
- Zeigt Richtung des Effekts an
- Erlaubt Aussagen über das Ausmaß erklärter Varianz (= Bestimmtheitsmaß r2 [ebenso für Regression von Bedeutung, R2])
- Weitere Koeffizienten aus der r-Familie sind Phi-Koeffizient, die punktbiseriale Korrelation und die Rangkorrelation - Cave: Einschränkungen des Koeffizienten (siehe z.B. Phi-Koeffizient) schlagen sich auch auf Einschätzung der Größe eines Effekts nieder
- Alle diese Koeffizienten können (prinzipiell) als Effektmaße verwendet und verstanden werden
- Auch die Produkt-Moment-Korrelation stellt Anforderungen an Daten: bivariate Normalverteilung, linearer Zusammenhang
Tags: Effektgröße, Produkt-Moment-Korrelation, r
Source: VO06
Source: VO06
Wie ist der Zusammenhang zwischen r und d?
r kann zudem in Cohens d umgerechnet werden und umgekehrt

Korrelative Herangehensweise und die Analyse von Mittelwertsunterschieden im allgemeinen linearen Modell (ALM) eigentlich dasselbe
(Hintergrund: Korrelationen (Zusammenhangshypothese) können als Mittelwertsunterschiede (Unterschiedshypothese) formuliert werden und umgekehrt)

Korrelative Herangehensweise und die Analyse von Mittelwertsunterschieden im allgemeinen linearen Modell (ALM) eigentlich dasselbe
(Hintergrund: Korrelationen (Zusammenhangshypothese) können als Mittelwertsunterschiede (Unterschiedshypothese) formuliert werden und umgekehrt)
Tags: Cohens d, Effektgröße, r
Source: VO06
Source: VO06
Wann spricht man bei r von einem kleinen, mittleren oder großen Effekt?
Faustregeln und Richtlinien zur Einschätzung der Größe eines Effekts: Cohen (1988), Lipsey und Wilson (2001)


- Lipsey und Wilson (2001) argumentieren, dass Angaben Cohens nicht korrekt - Umrechnung von d nach r ergibt Benchmarks von .10, .24, .37
- Um konsistent zu sein, können auch schon kleinere Koeffizienten als von Cohen angenommen für mittlere und große Effekte stehen
Tags: Cohens d, Effektgröße, r
Source: VO06
Source: VO06
Was ist das Effektmaß  ?
?
 ?
?- Eta2 (
 ) ist das „natürliche“ Effektmaß varianzanalytischer Untersuchungen
) ist das „natürliche“ Effektmaß varianzanalytischer Untersuchungen - Eta2 ist ein Maß dafür, wie viel Gesamtvarianz der abhängigen Variable durch den interessierenden Faktor (= unabhängige Variable) erklärt wird:
- Ergebnis ist ein Maß der Varianzaufklärung (Wertebereich 0 bis 1), das in der Interpretation vergleichbar ist mit r2

- Eta2 ist ein Globalmaß für Gesamteffekt eines Faktorsoder einer Wechselwirkung
- Auch gerade bei varianzanalytischen Designs ist jedoch häufig die Bestimmung des Unterschiedes spezifischer Gruppen informativer - D.h. zusätzlich zu Eta2 können/sollten in varianzanalytischen Designs auch andere Effektgrößen (z.B. Cohens d) bestimmt werden
Tags: Effektgröße, Eta
Source: VO07
Source: VO07
Was ist das 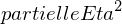 ? Wie ist der Zusammenhang zu
? Wie ist der Zusammenhang zu  ?
?
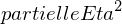 ? Wie ist der Zusammenhang zu
? Wie ist der Zusammenhang zu  ?
?Für mehrfaktorielle Designs wird auch das partielle Eta2 verwendet:


- Partielles Eta2 ist ein Maß der Varianzaufklärung unter Kontrolle (Herauspartialisierung) des Einflusses aller anderen Faktoren in der Gesamtvariabilität
- Wird von SPSS ausgegeben
- In einfaktoriellen Designs gilt: Eta2 = partielles Eta2
- In mehrfaktoriellen Designs gilt meist: Eta2 < partielles Eta2
- Interpretation als Maß der Varianzaufklärung bei partiellem Eta2 problematisch - Addiert man in mehrfaktoriellen Designs die partiellen Eta2 aller Faktoren und Wechselwirkungen kann die Summe > 1 (Varianzaufklärung > 100%) sein- Faktoren erklären scheinbar mehr Varianz als vorhanden ist
- Empfehlung, statt partiellem Eta2 lediglich Eta2 zu benutzen und zu berichten, da dies weniger verzerrt - Berechnung mit der Hand
Tags: Effektgröße, partielle Eta
Source: VO07
Source: VO07
Wie kann bei einer mixed ANOVA  berechnet werden?
berechnet werden?
 berechnet werden?
berechnet werden?In mixed design ANOVA gibt es zwei Fehlerterme (QSFehler für ZSF, QSRes für ISF und Wechselwirkung)
Berechnung von (partiellem) Eta2 getrennt für unabhängigen und abhängigen Faktor
Berechnung von (partiellem) Eta2 getrennt für unabhängigen und abhängigen Faktor
- Eta2 ein deskriptives Maß
- Statt Eta2 (= erklärte Varianz in der Stichprobe) wird deshalb häufiger auch vorgeschlagen, ω2 (Omega2 = Schätzer der erklärten Varianz in der Population) zu berechnen

Tags: Effektgröße, Eta, mixed ANOVA, partielle Eta
Source: VO07
Source: VO07
Wie können Effektgrößen für Kontraste berechnet werden?
Einerseits direkt über die entsprechenden QS (polynomiale Kontraste)

Andererseits auch über t- oder F-Werte der Kontrasttests (vgl. Field, 2009, S. 390, S. 532)

Quadrieren des oben erhaltenen Wertes erlaubt Angabe der erklärten Varianz (Cave: =
=  in diesem Fall !)
in diesem Fall !)

Andererseits auch über t- oder F-Werte der Kontrasttests (vgl. Field, 2009, S. 390, S. 532)

Quadrieren des oben erhaltenen Wertes erlaubt Angabe der erklärten Varianz (Cave:
 =
=  in diesem Fall !)
in diesem Fall !)Tags: Effektgröße, partielle Eta, r
Source: VO07
Source: VO07
Tags: Effektgröße, Eta
Source: VO07
Source: VO07
Was zeigt dieser SPSS-Ausdruck?


Effektstärken: Wie groß sind Effekte der Kontraste (Depressive vs. Remittierte & Gesunde, Remittierte vs. Gesunde; polynomiale Kontraste)?
Der Faktor Gruppe erklärt 65% der Gesamtvarianz
Im einfaktoriellen Design gilt: partielles Eta2 = Eta2.
Der Faktor Gruppe erklärt 65% der Gesamtvarianz
Im einfaktoriellen Design gilt: partielles Eta2 = Eta2.
Tags: Effektgröße, Eta, SPSS
Source: VO07
Source: VO07
Was sind die Effektgrößen für polynomiale Kontraste?
a) linearer Term?
b) quadratischer Term?
a) linearer Term?
b) quadratischer Term?
(gewichtete QS verwenden)
Linearer Term: Eta2 = 12082.501 / 19673.514 = .61
Quadratischer Term: Eta2 = 734.649 / 19673.514 = .04
Der Anteil der linearen Komponente ist 61%, jener der quadratischen 4% ergibt zusammen die 65% Varianzaufklärung des Faktors.
Polynomiale Komponenten sind orthogonal ... daher addieren sie sich zu Gesamteffekt des Faktors (dies sieht man im SPSS Ausdruck)

Linearer Term: Eta2 = 12082.501 / 19673.514 = .61
Quadratischer Term: Eta2 = 734.649 / 19673.514 = .04
Der Anteil der linearen Komponente ist 61%, jener der quadratischen 4% ergibt zusammen die 65% Varianzaufklärung des Faktors.
Polynomiale Komponenten sind orthogonal ... daher addieren sie sich zu Gesamteffekt des Faktors (dies sieht man im SPSS Ausdruck)

Tags: Effektgröße, Eta
Source: VO07
Source: VO07
Wie groß ist der Anteil an Varianz in Trait-Angst, der auf das Geschlecht, wie hoch jener, der auf das Vorliegen einer Angsterkrankung zurückgeführt werden kann?
Interpretiere es auf Basis dieses SPSS-Ausdrucks:

Interpretiere es auf Basis dieses SPSS-Ausdrucks:

- Partielles Eta2: Geschlecht erklärt 6% der Varianz, Gruppe 48%, Wechselwirkung < 1%
- Eta2 : QSTotal = QSGeschlecht + QSGruppe + QSGeschlecht * Gruppe + QSFehler = 21822.335(es wird die Gesamtvarianz berechnet und dann jeweils manuell die Varianz für jeden einzelnen Faktor)
- Geschlecht 3%, Gruppe 47%, Wechselwirkung < 1%
- Einfluss des Geschlechts tatsächlich nur halb so groß, verglichen mit partiellem Eta2 (Dass Eta2 ist kleiner als das partielle Eta2. Um einen Schätzer der Varianzerklärung zu erhalten soll Eta2 verwendet werden, damit es nicht zu einer Überschätzung kommt.)
Tags: Effektgröße, Eta, partielle Eta, SPSS
Source: VO07
Source: VO07

Zur Frage:
Wie groß sind Prä/Post-Differenzen, wie stark unterscheiden sich die Gruppen zu T1 und T2?
Was muss untersucht werden?
Was zeigen die SPSS Ausdrucke?


Betrachtet werden Eta2 als auch Cohens d.
Zu 1. SPSS Ausdruck - Tests der Innersubjekteffekte:
Partielles Eta2: addiert sich nicht auf 100% (> 100%) !
Zeit 87% der Varianz, Wechselwirkung 32%
Eta2 :
QSTotal_Innersubjekt = QSZeit + QSZeit * Behandlung + QSFehler(Zeit) = 11873.699
Zeit 82%, Wechselwirkung 6% (Wenn man auf die Partialisierung verzichtet hat man nur mehr ein Fünftel des Effekts!)
Zu 2. SPSS Ausdruck - Tests der Zwischensubjekteffekte:
Partielles Eta2: Behandlung 3% der Varianz
Eta2 :
QSTotal_Zwischensubjekt = QSBehandlung + QSFehler = 6012.600
Behandlung 3%
Partielles Eta2 und Eta2 sind hier wieder ident (nur ein Faktor in den Zwischensubjekteffekten)
Cohens d (berechnet mittels t-Tests):
Um die Effektivität der beiden Behandlungsarten im Pre-Post zu betrachten. Cohens d ist anschaulicher als Eta.
Effekt Prä/Post in CBT + Med deutlich größer als in CBT allein
Zu 1. SPSS Ausdruck - Tests der Innersubjekteffekte:
Partielles Eta2: addiert sich nicht auf 100% (> 100%) !
Zeit 87% der Varianz, Wechselwirkung 32%
Eta2 :
QSTotal_Innersubjekt = QSZeit + QSZeit * Behandlung + QSFehler(Zeit) = 11873.699
Zeit 82%, Wechselwirkung 6% (Wenn man auf die Partialisierung verzichtet hat man nur mehr ein Fünftel des Effekts!)
Zu 2. SPSS Ausdruck - Tests der Zwischensubjekteffekte:
Partielles Eta2: Behandlung 3% der Varianz
Eta2 :
QSTotal_Zwischensubjekt = QSBehandlung + QSFehler = 6012.600
Behandlung 3%
Partielles Eta2 und Eta2 sind hier wieder ident (nur ein Faktor in den Zwischensubjekteffekten)
Cohens d (berechnet mittels t-Tests):
Um die Effektivität der beiden Behandlungsarten im Pre-Post zu betrachten. Cohens d ist anschaulicher als Eta.
- Baseline-Testung CBT vs. CBT + Med: d = -0.37 (p = .057)
- Post-Testung CBT vs. CBT + Med: d = 0.78 (p < .001)
- CBT Prä/Post: d = 1.51 (p < .001) (Starker Effekt)
- CBT + Med Prä/Post: d = 2.74 (p < .001) (fast um 3-fache Standardabweichung besseres Ergebnis)
Effekt Prä/Post in CBT + Med deutlich größer als in CBT allein
Tags: Cohens d, Effektgröße, Eta, partielle Eta
Source: VO07
Source: VO07
Inwiefern können OR und RR als Effektmaße verwendet werden?
Inwiefern können diese in andere Effektmaße überführt werden?
Inwiefern können diese in andere Effektmaße überführt werden?
- OR und RR können ebenfalls als Effektmaße herangezogen werden
- Sie erlauben direkte Quantifizierung der Größe von Zusammenhängen und sind auch direkt anschaulich
- OR: Faktor, um den sich die Chancen eines Ereignisses in einer Gruppe gegenüber einer anderen Gruppe erhöhen/erniedrigen
- RR: Faktor, um den die Auftrittswahrscheinlichkeit (Inzidenz) eines Ereignisses durch Vorhandensein eines Risikofaktors erhöht/erniedrigt wird
- d, r und OR können ineinander umgerechnet werden - Anschaulichmachung kleiner/mittlerer/großer Effekte
OR und d
- Faustregeln zur Einschätzung der Größe eines Effekts (Cohen, 1988) gemäß der Umrechnung von d zu OR
- Referenzwerte nur für dichotome Variablen gut anwendbar
- In logistischer Regression ist ebenso OR das Zusammenhangs- und Effektmaß - obige Referenzwerte sind für kontinuierliche Prädiktoren nicht geeignet

RR und NNT
- RR kann nicht wie OR umgerechnet werden Eine damit zusammenhängende Effektgröße ist aber Number Needed to Treat (NNT; Anzahl der notwendigen Behandlungen)
- NNT = Anzahl jener Patienten, die mit Behandlung A behandelt werden müssen, damit gegenüber Behandlung B ein Patient mehr das gewünschte Therapieziel erreicht (komparative Maßzahl)
Tags: Cohens d, Effektgröße, NNT, odds ratio, risk ratio
Source: VO07
Source: VO07
Was ist NNT? Wertebereich? Wie wird diese berechnet?
- Eine mit dem risk ratio zusammenhängende Effektgröße ist Number Needed to Treat (NNT; Anzahl der notwendigen Behandlungen)
- Wichtige Kennzahl in der klinischen und Interventionsforschung
- Quantifiziert Überlegenheit einer Behandlung A (Testbehandlung) gegenüber einer Behandlung B (Kontrollbehandlung)
- NNT = Anzahl jener Patienten, die mit Behandlung A behandelt werden müssen, damit gegenüber Behandlung B ein Patient mehr das gewünschte Therapieziel erreicht (komparative Maßzahl)
Wertebereich
- Wertebereich der NNT von 1 bis unendlich - Sind Behandlung A und B (nahezu) gleichwertig - NNT große Zahl(Man muss unendliche viele Leute behandeln, damit eine Person das gewünschte Therapieziel erreicht).- Ist Behandlung A besser als B NNT kleine Zahl- Wenn Kontrollbehandlung besser als Testbehandlung NNT < 0 NNT < 0: Number Needed to Harm (NNH)... wird mit positivem Vorzeichen versehen (NNH = −NNT, wenn NNT < 0)... Wertebereich der NNH wiederum von 1 bis unendlich
Berechnung
- Berechnung der NNT über die sog. absolute Risikoreduktion (ARR; absolute risk reduction)
- NNT wird berechnet:
- NNT wird üblicherweise aufgerundet, wenn nicht ganzzahlig (ansonsten Überschätzung des Effekts)
 - ARR > 0 Behandlung A ist besser- ARR < 0 Behandlung B ist besser
- ARR > 0 Behandlung A ist besser- ARR < 0 Behandlung B ist besser Wenn ARR < 0 (Kontrollbehandlung besser als Testbehandlung) .... NNH = −NNT
Wenn ARR < 0 (Kontrollbehandlung besser als Testbehandlung) .... NNH = −NNTTags: Effektgröße, NNT
Source: VO07
Source: VO07
Was bedeutet ein Ergebnis für NNT von 3 für dieses Beispiel:

Was muss bei einer Interpretation von NNT beachtet werden?

Was muss bei einer Interpretation von NNT beachtet werden?
Hintergrund - Berechnung NNT:

Inhaltliche Interpretation:

Inhaltliche Interpretation:
- Bereits ab 3 Patienten, die mit CBT + Med (Behandlung A) behandelt werden, profitiert schon ein Patient mehr von dieser Behandlung, verglichen mit der reinen CBT-Behandlung (Behandlung B) großer Effekt der Behandlung A gegenüber B (NNT sehr klein)
- Generell hängt Interpretation der NNT von der Art der Störung oder Erkrankung und den verglichenen Behandlungen ab (vgl. McQuay & Moore, 1997)
- NNT ist damit deskriptive Maßzahl für den Vergleich zweier spezifischer Methoden im Hinblick auf ein spezifisches interessierendes Ereignis (Outcome) nicht uneingeschränkt über beliebige Untersuchungen vergleichbar!
Tags: Effektgröße, NNT
Source: VO07
Source: VO07
Welche Methoden gibt es zur Veranschaulichung von Cohens d?
Effektstärken können auf unterschiedliche Art veranschaulicht werden, um deren Interpretation zu erleichtern.
Für Cohens d z.B.
Nonoverlap = Angabe in Prozent, wie stark Verteilungen nicht überlappen

Perzentilvergleiche

(z.B. 0,7 Perzeptil: großer Effekt: Im Schnitt geht es einem Behandelten besser als 3/4 der unbehandelten Personen.)

Für Cohens d z.B.
- Binomial Effect Size Display (BESD; Rosenthal & Rubin, 1982)*<div style="padding-left:5px;">Nonoverlap und Overlap</div>* Perzentilvergleiche
Nonoverlap = Angabe in Prozent, wie stark Verteilungen nicht überlappen
- Großer Effekt - Nonoverlap groß - Verteilungen überlappen wenig* Kleiner Effekt - Nonoverlap klein - Verteilungen überlappen stark

Perzentilvergleiche

(z.B. 0,7 Perzeptil: großer Effekt: Im Schnitt geht es einem Behandelten besser als 3/4 der unbehandelten Personen.)

Wofür spielt die Spezifizierung der Größe von Effekten eine wichtige Rolle?
Spezifizierung der Größe von Effekten wichtig für die Planung (prospektiv) und zur Einschätzung der methodischen Güte (post hoc) von Studien - Festlegung eines N, das zum statistisch signifikanten Nachweis eines Effekts bestimmter Größe benötigt wird.


Tags: Effektgröße, Planung, Signifikanz
Source: VO07
Source: VO07
Was bedeutete diese Grafik:

Wie können die einzelnen Parameter festgelegt werden?

Wie können die einzelnen Parameter festgelegt werden?
Zusammenhang zwischen den einzelnen Parameter.
Kennt man 3 der 4 Parameter (oder legt sie fest), kann der 4. berechnet werden.
Festgelegt werden zur Ermittlung von N
Signifikanzniveau wird festgelegt basierend auf der Hypothese. (Häufig: 1% oder 5%)
Testmacht
Größe des Effekts kann üblicherweise
Festlegung der Effektgröße macht aus einer ansonsten unspezifischen H1 eine spezifische H1.
Um eine spezifische H1 bestmöglich (d.h. mit bekannter Power) zu testen, kann ein optimaler Stichprobenumfang bestimmt werden hilfreich für die Planung jeder empirischen Studie.
Bestimmung optimaler Stichprobenumfänge mithilfe von Tabellen (z.B. Bortz & Döring, 2002) oder Formeln (z.B. Bortz, 2008)
Kennt man 3 der 4 Parameter (oder legt sie fest), kann der 4. berechnet werden.
Festgelegt werden zur Ermittlung von N
- Signifikanzniveau (plus Entscheidung: einseitig/zweiseitig)
- Testmacht
- Effektgröße
Signifikanzniveau wird festgelegt basierend auf der Hypothese. (Häufig: 1% oder 5%)
Testmacht
- Wahrscheinlichkeit, dass H0 verworfen wird, wenn sie nicht gilt
- = 1 − β; β = Fehler 2. Art = Wahrscheinlichkeit, dass H0 nicht verworfen wird, obwohl sie in der Population nicht gilt
- Testmacht wird üblicherweise mit .80 festgelegt (vgl. Cohen, 1988: α : β = 1 : 4; wenn α = .05 β = .20 1 − β = .80)
Größe des Effekts kann üblicherweise
- inhaltlich begründet festgelegt werden
- aus Vorstudien erschlossen werden
- anhand konventioneller Cutoffs festgelegt werden (z.B. Cutoffs von Cohen): z.B. im Rahmen der Forschung zu psychologischen Interventionen ist die Annahme eines großen Behandlungseffektes (d » 0.8) häufig angemessen
Festlegung der Effektgröße macht aus einer ansonsten unspezifischen H1 eine spezifische H1.
Um eine spezifische H1 bestmöglich (d.h. mit bekannter Power) zu testen, kann ein optimaler Stichprobenumfang bestimmt werden hilfreich für die Planung jeder empirischen Studie.
Bestimmung optimaler Stichprobenumfänge mithilfe von Tabellen (z.B. Bortz & Döring, 2002) oder Formeln (z.B. Bortz, 2008)
- Direkt anwendbar für alle möglichen Analysearten (z.B. t-Test, ANOVA, Korrelation, Regression, etc.)
- Empfehlenswertes frei verfügbares Programm: G*Power
Tags: Effektgröße, Optimaler Stichprobenumfang, Signifikanz, Testmacht
Source: VO07
Source: VO07
Wie ist der Zusammenhang zwischen N und Effektgröße (bei fixer Signfikanz und Testmacht)?
α = .05 einseitig / Testmacht 1 − β = .80
Benötigtes n pro Gruppe, um einen Effekt gewählter Größe mit einer Testmacht von 80% und bei einseitiger Testung mit einer Fehlerwahrscheinlichkeit von 5% statistisch signifikant nachweisen zu können.


Benötigtes n pro Gruppe, um einen Effekt gewählter Größe mit einer Testmacht von 80% und bei einseitiger Testung mit einer Fehlerwahrscheinlichkeit von 5% statistisch signifikant nachweisen zu können.


Tags: Effektgröße, Optimaler Stichprobenumfang, Stichprobe
Source: VO07
Source: VO07
Was ist der Zusammenhang zwischen der Stichprobengröße (N) und das Verwerfen der H0?
Wechselseitige Zusammenhänge zwischen N, Power, Effektgröße und Signifikanzniveau veranschaulichen noch ein weiteres Phänomen:
Mit steigendem N wird jede beliebige H0 mit Sicherheit verworfen
Veranschaulichung Zusammenhang N und p
Bsp.: Mittelwertsvergleich, t-Test für unabhängige Stichproben
M1= 100, M2 = 105, SDpooled = 25
...kleiner Effekt (d = 0.2)


Ist inhaltliche Interpretation, dass Effekt von d = 0.2 im gegebenen Fall bedeutsam, dann sind Studien dieser Größe schlicht zu klein und underpowered, um ihn zu belegen.
Unterste zwei Zeilen:
Ist inhaltliche Interpretation, dass Effekt von d = 0.2 im gegebenen Fall unbedeutend, dann erbringen Studien dieser Größe irrelevante signifikante Ergebnisse.
Mit steigendem N wird jede beliebige H0 mit Sicherheit verworfen
- Ist Stichprobe groß genug, kann jeder beliebig kleine Effekt signifikant werden
- Andererseits: selbst wenn ein Effekt existiert, kann die Stichprobe schlicht zu klein sein, um Signifikanz erreichen zu können underpowered study
- Verwerfen der H0 bedeutet nicht unbedingt, dass ein bedeutsamer Effekt gefunden wurde
- Beibehalten der H0 bedeutet nicht unbedingt, dass kein Effekt existiert
Veranschaulichung Zusammenhang N und p
Bsp.: Mittelwertsvergleich, t-Test für unabhängige Stichproben
M1= 100, M2 = 105, SDpooled = 25
...kleiner Effekt (d = 0.2)


Ist inhaltliche Interpretation, dass Effekt von d = 0.2 im gegebenen Fall bedeutsam, dann sind Studien dieser Größe schlicht zu klein und underpowered, um ihn zu belegen.
Unterste zwei Zeilen:
Ist inhaltliche Interpretation, dass Effekt von d = 0.2 im gegebenen Fall unbedeutend, dann erbringen Studien dieser Größe irrelevante signifikante Ergebnisse.
Tags: Effektgröße, Optimaler Stichprobenumfang, Signifikanz, Stichprobe
Source: VO08
Source: VO08
Was versteht man unter underpowered study?
Selbst wenn ein Effekt existiert, kann die Stichprobe schlicht zu klein sein, um Signifikanz erreichen zu können ... underpowered study:
Beibehalten der H0 bedeutet nicht unbedingt, dass kein Effekt existiert.
Beibehalten der H0 bedeutet nicht unbedingt, dass kein Effekt existiert.
Tags: Optimaler Stichprobenumfang, Signifikanz
Source: VO08
Source: VO08
Inwiefern hilft die Effektgröße hinsichtlich des korrekten Verwerfens bzw. Beibehalten der H0?
Verwendung von Effektgrößen hilft
Wichtig: Eine Einschätzung von Effektgrößen ist keine willkürliche, sondern soll empirisch betrieben werden (gut begründen)
- inhaltlich unbedeutende Effekte (trotz ihrer möglichen Signifikanz) als solche zu erkennen
- Hinweise auf das Vorliegen hypothesenkonformer Effekte zu erhalten, selbst wenn Studie möglicherweise underpowered war (nicht-signifikantes Ergebnis)
Wichtig: Eine Einschätzung von Effektgrößen ist keine willkürliche, sondern soll empirisch betrieben werden (gut begründen)
Tags: Effektgröße, Signifikanz
Source: VO08
Source: VO08
Wie wird die Testmacht (Power) festgelegt bzw. wie kann dies vergrößert werden?
Bei Fixierung von Signifikanzniveau, Effektgröße und N kann Power einer Studie berechnet werden
- Aussagen dazu, ob eine Untersuchung mit gegebenem N genug Power besitzt, um einen angenommenen Effekt nachweisen zu können
Hohe Power für empirische Untersuchungen eminent wichtig – wozu überhaupt eine Untersuchung machen, wenn keine reelle Chance für den Erhalt eines verwertbaren (= statistisch bedeutsamen) Ergebnisses besteht?
Power ist nicht nur an N gebunden.
Power lässt sich ebenso durch Studiendesign vergrößern
Poweranalysen (a priori Berechnungen der Stichprobengröße) sind in moderner klinischer Forschung Standard - (obligatorischer) Teil von Studienprotokollen und Anträgen für
Forschungsförderung.
- Aussagen dazu, ob eine Untersuchung mit gegebenem N genug Power besitzt, um einen angenommenen Effekt nachweisen zu können
Hohe Power für empirische Untersuchungen eminent wichtig – wozu überhaupt eine Untersuchung machen, wenn keine reelle Chance für den Erhalt eines verwertbaren (= statistisch bedeutsamen) Ergebnisses besteht?
Power ist nicht nur an N gebunden.
Power lässt sich ebenso durch Studiendesign vergrößern
- Vergrößerung zu untersuchender Effekte - Untersuchung homogener Samples – dadurch werden zufällige Varianzen kleiner und die Mittelwertsunterschiede größer- Matching und Parallelisierung: Varianzen werden hier reduziert. – Effekt wird vergrößert- Untersuchung von Extremgruppen: innerhalb der beiden Gruppen sind diese homogen.- Erhöhung der Dosis: mehr oder längere Interventionen- Outcomes untersuchen, die am direktesten das interessierende Konstrukt abbilden/repräsentieren
- Reduzierung des Messfehlers - Messinstrumente mit kleinem Messfehler verwenden, d.h. Instrumente mit nachgewiesen hoher Reliabilität
- (Erhöhung von α) wird man eher nicht erhöhen, da auch der Fehler 2. Art erhöht (Verwerfen der H0 obwohl die H0 gilt) wird
Poweranalysen (a priori Berechnungen der Stichprobengröße) sind in moderner klinischer Forschung Standard - (obligatorischer) Teil von Studienprotokollen und Anträgen für
Forschungsförderung.
Tags: Power, Testmacht
Source: VO08
Source: VO08
Was versteht man unter Beurteilerübereinstimmung? In welchen Fällen ist diese notwendig?
Erhebungsmethoden in der empirischen Forschung und klinischen
Psychologie nicht auf Selbstberichte (z.B. standardisierte Fragebögen) beschränkt.
Fremdbeurteilungen durch i. d. R. geschulte Rater stellen eine weitere wichtige Informationsquelle dar, z.B.:
Analog zur Messgüte bei Fragebogenverfahren (Validität, Reliabilität, etc.) stellt sich auch bei Fremdbeurteilungen die Frage nach deren Güte
INTERRATERRELIABILITÄT
Kommen zwei (oder mehr) Beurteiler unabhängig voneinander zur
gleichen Einschätzung/Diagnose ?
Psychologie nicht auf Selbstberichte (z.B. standardisierte Fragebögen) beschränkt.
Fremdbeurteilungen durch i. d. R. geschulte Rater stellen eine weitere wichtige Informationsquelle dar, z.B.:
- Beim Stellen von Diagnosen
- Für die klinische Einschätzung von Schweregraden (z.B. HRSD)
- Allgemein zur Einschätzung der Ausprägung beliebiger Merkmale
Analog zur Messgüte bei Fragebogenverfahren (Validität, Reliabilität, etc.) stellt sich auch bei Fremdbeurteilungen die Frage nach deren Güte
INTERRATERRELIABILITÄT
Kommen zwei (oder mehr) Beurteiler unabhängig voneinander zur
gleichen Einschätzung/Diagnose ?
Tags: Interraterreliabilität
Source: VO08
Source: VO08
Was versteht man unter der Interraterreliabilität und welche Aussagen liefert sie?
INTERRATERRELIABILITÄT
Kommen zwei (oder mehr) Beurteiler unabhängig voneinander zur
gleichen Einschätzung/Diagnose ?
(notwendig bei Fremdbeurteilungen)
Interraterreliabilität liefert Aussagen hinsichtlich
Urteile sollten davon unabhängig sein, wer sie vergeben hat
(vgl. Wirtz & Caspar, 2002, S. 15)
Kommen zwei (oder mehr) Beurteiler unabhängig voneinander zur
gleichen Einschätzung/Diagnose ?
(notwendig bei Fremdbeurteilungen)
Interraterreliabilität liefert Aussagen hinsichtlich
- Genauigkeit von Urteilen
- Objektivität (sind Urteile unabhängig von der Person des jeweiligen Raters?)
Urteile sollten davon unabhängig sein, wer sie vergeben hat
(vgl. Wirtz & Caspar, 2002, S. 15)
- (prinzipielle) Austauschbarkeit der Rater
- Urteile eines Raters ausreichend
- Urteile spiegeln „wahre Merkmalsausprägung“ (klassische Testtheorie) reliabel wider
Tags: Interraterreliabilität
Source: VO08
Source: VO08
Wie kann die Interraterreliabiltät berechnet werden? Voraussetzungen?
Erfassung und Untersuchung der Interraterreliabilität setzt voraus, dass
Interraterreliabilität kann dann mithilfe von Maßen der Beurteilerübereinstimmung berechnet werden.
Unterscheidung gemäß Skalenniveau und anhand der jeweils
verwendeten Definition von Übereinstimmung
Konkordanz bezieht sich i. A. auf die (absolute) Gleichheit von Urteilen,
Reliabilität auf die Ähnlichkeit (relative Gleichheit) von Urteilen.
- mindestens zwei Rater
- Urteile zu denselben Objekten abgegeben haben
Interraterreliabilität kann dann mithilfe von Maßen der Beurteilerübereinstimmung berechnet werden.
Unterscheidung gemäß Skalenniveau und anhand der jeweils
verwendeten Definition von Übereinstimmung
- nominale/ordinale Skalen: Konkordanz
- metrische Skalen: Reliabilität i. e. S.
Konkordanz bezieht sich i. A. auf die (absolute) Gleichheit von Urteilen,
Reliabilität auf die Ähnlichkeit (relative Gleichheit) von Urteilen.
Tags: Interraterreliabilität
Source: VO08
Source: VO08
Was versteht man unter
a) Konkordanz?
b) Reliabilität?
a) Konkordanz?
b) Reliabilität?
(Interraterreliabilität - Beurteilerübereinstimmung)
Konkordanz bezieht sich i. A. auf die (absolute) Gleichheit von Urteilen,
Reliabilität auf die Ähnlichkeit (relative Gleichheit) von Urteilen.
(Gut = Sehr gut / Genügend != Sehr gut)
Konkordanz bezieht sich i. A. auf die (absolute) Gleichheit von Urteilen,
Reliabilität auf die Ähnlichkeit (relative Gleichheit) von Urteilen.
(Gut = Sehr gut / Genügend != Sehr gut)
Tags: Interraterreliabilität, Konkordanz, Reliabilität
Source: VO08
Source: VO08
Was ist die Konkordanz?
- Interraterreliabilität, Beurteilungsübereinstimmung
- Anwendung auf nominalskalierte (kategoriale) Merkmale (z.B. Diagnosen)
- Erfassung des Ausmaßes der Gleichheit von Urteilen
Tags: Interraterreliabilität, Konkordanz
Source: VO08
Source: VO08
Welche Rolle spielt die Interraterreliabilität in der Diagnostik? In welchen Fällen ist keine Übereinstimmung erwartbar?
Diagnostik in der klinischen Psychologie basiert häufig auf der Anwendung strukturierter klinischer Interviews
Operationalisierte und standardisierte Diagnostik psychischer Störungen
Aber: Werden spezifische Diagnosen von unterschiedlichen Ratern nach Durchführung des Interviews übereinstimmend vergeben ?
Nicht-Übereinstimmungen i. A. erwartbar
Operationalisierte und standardisierte Diagnostik psychischer Störungen
- Objektiv (Standardisierung, Raterschulung)
- Valide (operationalisierte Diagnostik nach ICD-10 und/oder DSM-IV)
Aber: Werden spezifische Diagnosen von unterschiedlichen Ratern nach Durchführung des Interviews übereinstimmend vergeben ?
Nicht-Übereinstimmungen i. A. erwartbar
- Ebene der Operationalisierung (z.B. unpräzise Diagnosekriterien)
- Ebene des Durchführenden (z.B. Symptomgewichtung, Anwendungsfehler)
- Ebene des Interviewten (z.B. unterschiedliche Offenheit)
Tags: Interraterreliabilität
Source: VO08
Source: VO08
Was zeigte die Untersuchung des DIPS - wie kann die Konkordanz berechnet werden:

Was ist bei der Berechnung bzw. Interpretation der Konkordanz zu beachten?

Was ist bei der Berechnung bzw. Interpretation der Konkordanz zu beachten?
DIPS (Diagnostisches Interview bei psychischen Störungen; Schneider & Margraf, 2005): Erlaubt die standardisierte Diagnostik einer Anzahl definierter Störungsbilder nach ICD-10 und DSM-IV-TR
Angaben zur Konkordanz (in Bezug auf Lebenszeitdiagnosen) geschulter Rater im Manual (N = 237 Patienten)
Einfachste Möglichkeit der Konkordanzbestimmung

(Also 13% nicht übereinstimmende Resultate)
Angaben zur Konkordanz (in Bezug auf Lebenszeitdiagnosen) geschulter Rater im Manual (N = 237 Patienten)
Einfachste Möglichkeit der Konkordanzbestimmung

(Also 13% nicht übereinstimmende Resultate)
- Prozentuale Übereinstimmung einfaches und anschauliches Maß
- Allerdings: aus statistischer Sicht ist auch dann mit Übereinstimmungen zu rechnen, wenn Rater Urteile völlig zufällig vergeben (vgl. Analyse von Vier-Felder-Tafeln, χ2-Tests)
- Zufällige Übereinstimmungen werden in prozentualer Übereinstimmung nicht berücksichtigt und können somit zu einer Überschätzung der Konkordanz führen ... man kann jetzt folgendes verwenden: Cohens Kappa
Tags: Interraterreliabilität, Konkordanz
Source: VO08
Source: VO08
Was ist Cohens Kappa? Welche Maßzahlen können berechnet werden?
Bei einer einfachen Konkordanzbestimmung mittels prozentueller Darstellung werden zufällige Übereinstimmungen nicht berücksichtigt und können somit zu einer Überschätzung der
Konkordanz führen - deshalb Verwendung von Cohens Kappa.

- P0 = beobachteten Urteile
- Pe = erwartenden Urteile
Konkordanz führen - deshalb Verwendung von Cohens Kappa.
- Cohens Kappa (κ) ist ein zufallsbereinigtesMaß der Beurteilerübereinstimmung (Konkordanz) für 2 Rater (Cohen, 1960)
- Ähnlich wie für χ2-Tests wird für die Berechnung von Kappa die Anzahl zufällig konkordanter Urteile aus den Randverteilungen geschätzt (unter Annahme der Unabhängigkeit der Urteile)

- P0 = beobachteten Urteile
- Pe = erwartenden Urteile
Tags: Cohens Kappa, Interraterreliabilität
Source: VO08
Source: VO08
In welchem Wertebereich kann das Cohens Kappa liegen?
- Wertebereich von Kappa −1 bis +1
- Ähnlich Korrelation, allerdings mit anderer Interpretation negativer Werte
- κ = +1: Perfekte Übereinstimmung/Konkordanz (b = c = 0 .... p0 = 1)
- κ = −1: keine beobachteten Übereinstimmungen (a = d = 0 ... p0 = 0) bei maximaler Wahrscheinlichkeit zufälliger Übereinstimmungen (b = c .... pe = 0.5 ... alle vier Randsummen sind identisch)
- κ = 0: beobachtete Übereinstimmung ist nicht besser als die durch den Zufall erwartete (p0 = pe)

Tags: Cohens Kappa, Interraterreliabilität
Source: VO08
Source: VO08
Was zeigt dieser SPSS-Ausdruck:




Beispiel: 2 Rater und wie sie Major Depression diagnostiziert haben

Kappa = .73, p < .001 (einseitig)
Spricht ein Kappa von .73 für eine gute Konkordanz? - Ja.

Kappa = .73, p < .001 (einseitig)
Spricht ein Kappa von .73 für eine gute Konkordanz? - Ja.
Tags: Cohens Kappa, Interraterreliabilität, SPSS
Source: VO08
Source: VO08
Wann spricht man guter Konkordanz bei Cohens Kappa? Was ist bei der Interpretation der Werte zu beachten?
Cutoffs für Kappa (Fleiss, 1981) – Signifikanz vorausgesetzt

Allerdings: Wertebereich und Ausprägung des Koeffizienten von einer Anzahl an Faktoren beeinflusst, die nicht Konkordanz selbst betreffen .... erschwert Interpretation von Kappa und verringert den Nutzen von Cutoffs
Kappa beeinflusst durch
Effekte gehen in gleiche Richtung .... i. A. Unterschätzung der Konkordanz

Allerdings: Wertebereich und Ausprägung des Koeffizienten von einer Anzahl an Faktoren beeinflusst, die nicht Konkordanz selbst betreffen .... erschwert Interpretation von Kappa und verringert den Nutzen von Cutoffs
Kappa beeinflusst durch
- Randverteilungen (vgl. Phi-Koeffizient)
- Anzahl der Kategorien und der Besetzung von Zellen
- Prävalenz des untersuchten Merkmals
Effekte gehen in gleiche Richtung .... i. A. Unterschätzung der Konkordanz
Tags: Cohens Kappa, Interraterreliabilität
Source: VO08
Source: VO08
Wodurch wird das Cohens Kappa beeinflusst?
Wertebereich und Ausprägung des Koeffizienten von einer Anzahl an Faktoren beeinflusst, die nicht Konkordanz selbst betreffen ... erschwert Interpretation von Kappa und verringert den Nutzen von Cutoffs
Kappa beeinflusst durch
Effekte gehen in gleiche Richtung i. A. .... Unterschätzung der Konkordanz
Kappa beeinflusst durch
- Randverteilungen (vgl. Phi-Koeffizient) .... i. A. Unterschätzung der Konkordanz bei ungleichen Randverteilungen
- Anzahl der Kategorien und der Besetzung von Zellen (Asendorpf & Wallbott, 1978)- geringe Anzahl an Beurteilungskategorien und/oder nur geringe Zellbesetzungen .... Unterschätzung der Konkordanz(Je weniger Kategorien oder geringe Werte in den Zellen (kleiner als 5) desto weniger Konkordanz)
- Prävalenz des untersuchten Merkmals (Feinstein & Cicchetti, 1990; Spitznagel & Helzer, 1985)bei niedriger Prävalenz (ca. < 10% in der Stichprobe) ... Unterschätzung der Konkordanz
Effekte gehen in gleiche Richtung i. A. .... Unterschätzung der Konkordanz
Tags: Cohens Kappa, Interraterreliabilität, Konkordanz
Source: VO08
Source: VO08
Welche weiteren Varianten des Cohens Kappa können berechnet werden? Welche anderen Koeffizienten sind noch zu empfehlen?
Berechnung des gewichteten Kappa (weighted Kappa;
Cohen, 1968)
Kappa verrechnet alle Nicht-Übereinstimmungen gleich schwer, kann unangemessen sein, wenn Merkmale z.B. ordinal skaliert sind
Fleiss‘ Kappa
Probleme des Kappa-Koeffizienten führten auch zur Empfehlung der Verwendung anderer Koeffizienten
Cohen, 1968)
Kappa verrechnet alle Nicht-Übereinstimmungen gleich schwer, kann unangemessen sein, wenn Merkmale z.B. ordinal skaliert sind
Fleiss‘ Kappa
- Liegen Urteile von mehr als 2 Ratern vor und ist man an deren Übereinstimmung interessiert
- Mittlere Konkordanz aller Rater über alle Objekte
- Inhaltlich kann Fleiss‘ Kappa analog zu Cohens Kappa interpretiert werden, Gewichtung ist aber nicht möglich
Probleme des Kappa-Koeffizienten führten auch zur Empfehlung der Verwendung anderer Koeffizienten
- Für dichotome Ratingsskalen und 2 Rater z.B. Odds Ratio oder Yules Y (vgl. Wirtz & Caspar, 2002)
- Für metrische Ratingskalen ist insbesondere die Intraklassenkorrelation (ICC) ein gebräuchliches Maß zur Bestimmung der Interraterreliabilität - Maß der Varianzaufklärung (Wertebereich 0 bis 1)- Für 2 oder mehr Rater geeignet- Erlaubt Bestimmung der absoluten oder der relativen Gleichheit von UrteilenIn SPSS (Analysieren > Skalieren > Reliabilitätsanalyse …) ausreichend implementiert
Tags: Cohens Kappa, Interraterreliabilität
Source: VO08
Source: VO08
Wann sollen nicht-parametrische Verfahren eingesetzt werden?
Parametrische Verfahren (z.B. F-Test, t-Test, ANOVA) wichtigste statistische Methoden der empirischen Forschung - aber haben Voraussetzungen
Nicht-parametrische Verfahren sind hingegen i. d. R. voraussetzungsärmer
- Parametrische Verfahren eignen sich aber nicht für alle Daten - Skalenniveau der abhängige Variable (AV) muss metrisch sein
- Stellen Anforderungen an die Verteilung und einzelne Parameter der Daten („parametrische Verfahren“); typischerweise: - Normalverteilung- Varianzhomogenität
- Voraussetzungsverletzungen können Typ-I- und Typ-II-Fehlerhäufigkeiten beeinflussen
Nicht-parametrische Verfahren sind hingegen i. d. R. voraussetzungsärmer
- Benötigen nicht unbedingt metrische Daten
- Kommen häufig ohne Annahmen zur Verteilung aus
- Mathematische Grundlage nicht-parametrischer Verfahren aber heterogen und uneinheitlich (kein „allgemeines lineares Modell“ für nicht-parametrischen Verfahren)
- Häufig wird Ranginformation der Daten verwendet
Tags: nicht-parametrische Verfahren, parametrische Verfahren
Source: VO09
Source: VO09
Was ist der unterschied zwischen parametrischen und nicht-parametrischen Verfahren hinsichtlich
- Effizienz
- Messniveau
- Voraussetzungen
- Effizienz
- Messniveau
- Voraussetzungen
Effizienz
Messniveau
Mathematisch-statistische Voraussetzungen
- Prüfung der Voraussetzungen für parametrische Tests jedoch häufig problematisch
- Erfolgt i. d. R. anhand der Stichprobe
- Voraussetzungen beziehen sich aber eigentlich auf Populationscharakteristika
- Bei Zutreffen ihrer Voraussetzungen haben parametrische Verfahren i. A. eine größere Effizienz - höhere Testmacht (p-Werte kleiner)
- Treffen Voraussetzungen nicht zu nicht-parametrische Methoden i. d. R. effizienter
Messniveau
- Metrisches Messniveau für parametrische Tests
- für alle anderen Skalenniveaus muss nicht-parametrisch getestet werden
Mathematisch-statistische Voraussetzungen
- Parametrische Verfahren stellen immer Voraussetzungen an die Verteilung der Daten
- Nicht-parametrische Verfahren benötigen ebenso öfter stetige Variablen und häufig auch die Homogenität der Populationsverteilungen
- Prüfung der Voraussetzungen für parametrische Tests jedoch häufig problematisch
- Erfolgt i. d. R. anhand der Stichprobe
- Voraussetzungen beziehen sich aber eigentlich auf Populationscharakteristika
Tags: nicht-parametrische Verfahren, parametrische Verfahren, Voraussetzungen
Source: VO09
Source: VO09
Welche Probleme gibt es bei Voraussetzungstest für parametrische Verfahren?
Prüfung der Voraussetzungen für parametrische Tests jedoch häufig problematisch: Erfolgt i. d. R. anhand der Stichprobe, Voraussetzungen beziehen sich aber eigentlich auf Populationscharakteristika
Probleme von Voraussetzungstests
Werden kleine Stichproben untersucht, können Voraussetzungen parametrischer Verfahren häufig nur ungenügend untersucht werden
Autoren wie Bortz und Lienert (2008, S. 59) plädieren deshalb dafür, bei kleineren Stichproben (N < 30) grundsätzlich nicht-parametrisch zu testen
Zentrales Grenzwerttheorem
Besagt, dass z.B. Mittelwerte sich ab etwa N = 30 normalverteilen, unabhängig von eigentlicher Verteilung der Messwerte - trägt zur Robustheit parametrischer Verfahren bei
Generell lässt sich folgern, dass, wenn nur kleine Stichproben (N < 30) untersucht werden können (vgl. Bortz & Lienert, 2008, S. 52)
Probleme von Voraussetzungstests
- beruhen meist ebenso auf parametrischen Voraussetzungen z.B. F-Test zur Überprüfung der Homogenität von Varianzen beruht auf der Annahme der Normalverteilung der Daten
- ' Stichprobengröße (vgl. Kapitel zu Effektgrößen) - kleines N - geringe Testmacht - Verletzungen werden u. U. nicht erkannt- großes N - hohe Testmacht - bereits unbedeutende Abweichungen werden auffällig
Werden kleine Stichproben untersucht, können Voraussetzungen parametrischer Verfahren häufig nur ungenügend untersucht werden
Autoren wie Bortz und Lienert (2008, S. 59) plädieren deshalb dafür, bei kleineren Stichproben (N < 30) grundsätzlich nicht-parametrisch zu testen
Zentrales Grenzwerttheorem
Besagt, dass z.B. Mittelwerte sich ab etwa N = 30 normalverteilen, unabhängig von eigentlicher Verteilung der Messwerte - trägt zur Robustheit parametrischer Verfahren bei
Generell lässt sich folgern, dass, wenn nur kleine Stichproben (N < 30) untersucht werden können (vgl. Bortz & Lienert, 2008, S. 52)
- Nicht-parametrisch getestet werden sollte
- Möglichst große Effekte untersucht werden sollten
- Signifikante Ergebnisse i. d. R. auch auf große Effekte schließen lassen - Replikation wichtig !
Tags: nicht-parametrische Verfahren, parametrische Verfahren, Voraussetzungen
Source: VO09
Source: VO09
Was besagt das zentrale Grenzwerttheorem?
Zentrales Grenzwerttheorem
Besagt, dass z.B. Mittelwerte sich ab etwa N = 30 normalverteilen, unabhängig von eigentlicher Verteilung der Messwerte - trägt zur Robustheit parametrischer Verfahren bei.
Bei größeren Stichproben (N > 30) sind insbesondere Verteilungsannahmen für parametrische Tests häufig vernachlässigbar.
Generell lässt sich folgern, dass, wenn nur kleine Stichproben (N < 30) untersucht werden können (vgl. Bortz & Lienert, 2008, S. 52)
Besagt, dass z.B. Mittelwerte sich ab etwa N = 30 normalverteilen, unabhängig von eigentlicher Verteilung der Messwerte - trägt zur Robustheit parametrischer Verfahren bei.
Bei größeren Stichproben (N > 30) sind insbesondere Verteilungsannahmen für parametrische Tests häufig vernachlässigbar.
Generell lässt sich folgern, dass, wenn nur kleine Stichproben (N < 30) untersucht werden können (vgl. Bortz & Lienert, 2008, S. 52)
- Nicht-parametrisch getestet werden sollte
- Möglichst große Effekte untersucht werden sollten
- Signifikante Ergebnisse i. d. R. auch auf große Effekte schließen lassen - Replikation wichtig !
Tags: nicht-parametrische Verfahren, parametrische Verfahren, Stichprobe
Source: VO09
Source: VO09
Was sind Nachteile nicht-parametrischer Verfahren?
Größerer Nachteil nicht-parametrischer Verfahren:
Nicht jeder parametrische Test hat eine nicht-parametrische Entsprechung
Multivariate (mehr als eine AV) und multifaktorielle Designs (mehr als eine UV) häufig nicht nicht-parametrisch testbar.
In der Praxis:
Weiterer Nachteil nicht-parametrischer Verfahren:
Jedoch weisen die meisten nicht-parametrischen Tests asymptotische Eigenschaften auf
Nicht jeder parametrische Test hat eine nicht-parametrische Entsprechung
Multivariate (mehr als eine AV) und multifaktorielle Designs (mehr als eine UV) häufig nicht nicht-parametrisch testbar.
In der Praxis:
- Transformation der Daten, damit Verteilungsannahmen eher zutreffen (Log-/Wurzel-/Power-Transformationen, Box-Cox-Transformationen)
- Verwendung parametrischer Methoden, die nicht Normalverteilung oder Varianzhomogenität benötigen (z.B. linear mixed models, generalized mixed models)
Weiterer Nachteil nicht-parametrischer Verfahren:
- Effektstärken undefiniert
- p-Werte müssen (bei händischer Berechnung) bei kleinem N aus Tabellen abgelesen werden, da sie auf Permutationen und nicht auf definierten Prüfverteilungen (z.B. t-Verteilung) beruhen
Jedoch weisen die meisten nicht-parametrischen Tests asymptotische Eigenschaften auf
- wenn N genügend groß, folgen Teststatistiken definierten Verteilungen z.B. Standardnormalverteilung, χ2-Verteilung
- Dadurch können Power- und Effektstärkenberechnungen approximativ durchgeführt werden (vgl. Bortz & Lienert, 2008, S. 48f.)
Tags: nicht-parametrische Verfahren, parametrische Verfahren
Source: VO09
Source: VO09
Was sind Beispiele (5) für nicht-parametrische Verfahren?
- Mediantest H0: Die beiden Stichproben stammen aus Populationen mit gleichem Median bzw.H0: Die k Stichproben stammen aus Populationen mit gleichem Median
- U-Test H0: Die beiden Stichproben stammen aus formgleich (homomer) verteilten Populationen mit gleichem Median
- Kruskal-Wallis-Test ist Verallgemeinerung der Prinzipien des U-Test für k > 2 Stichproben („klassisches“ Pendant der einfaktoriellen ANOVA)H0: Die k Stichproben stammen aus formgleich (homomer) verteilten Populationen mit gleichem Median
- Jonckheere-Terpstra-Test H1: Die Mediane der k Stichproben folgen einer schwach monotonen Rangordnung:
- McNemar-Test ist einfachstes nicht-parametrisches Verfahren zur Untersuchung dichotomer Merkmale in 2 abhängigen Stichproben (Test zweier abhängiger prozentualer Anteile)
 (an zumindest einer Stelle muss das „
(an zumindest einer Stelle muss das „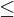 “ durch ein „
“ durch ein „ “ ersetzbar sein)
“ ersetzbar sein)Tags: nicht-parametrische Verfahren
Source: VO09, VO10
Source: VO09, VO10
Was prüft der Mediantest?
Nicht-parametrische Verfahren / 2 unabhängige Stichproben
Mediantest prüft 2 unabhängige Stichproben auf Unterschiede in ihrer zentralen Tendenz (ist – neben U-Test – eine nicht-parametrische Entsprechung zum t-Test für unabhängige Stichproben)
H0: Die beiden Stichproben stammen aus Populationen mit gleichem Median
Verwendet Ranginformation der Daten geeignet für (originär)
ordinalskalierte und metrische abhängige Variablen
Mediantest ist i. A. der schwächste nicht-parametrische Test zur Untersuchung von Lageunterschieden.
Allerdings: sehr robust gegenüber Ausreißern, macht keinerlei Annahmen zur Form oder Homogenität der Verteilung in den Stichproben
Mediantest prüft 2 unabhängige Stichproben auf Unterschiede in ihrer zentralen Tendenz (ist – neben U-Test – eine nicht-parametrische Entsprechung zum t-Test für unabhängige Stichproben)
H0: Die beiden Stichproben stammen aus Populationen mit gleichem Median
Verwendet Ranginformation der Daten geeignet für (originär)
ordinalskalierte und metrische abhängige Variablen
Mediantest ist i. A. der schwächste nicht-parametrische Test zur Untersuchung von Lageunterschieden.
Allerdings: sehr robust gegenüber Ausreißern, macht keinerlei Annahmen zur Form oder Homogenität der Verteilung in den Stichproben
Tags: Medientest, nicht-parametrische Verfahren
Source: VO09
Source: VO09
Wie wird der Mediantest durchgeführt?
Mediantest prüft 2 unabhängige Stichproben auf Unterschiede in ihrer zentralen Tendenz
Prinzip:


Gruppe A und B unterscheiden sich signifikant hinsichtlich ihrer zentralen Tendenz
Prinzip:
- Für beide Stichproben wird ein gemeinsamer Median bestimmt
- Auszählen, wie viele Messwerte in den jeweiligen Stichproben über und unter diesem Wert liegen
- Durchführen eines Vier-Felder-Tests (exakt oder asymptotisch)


Gruppe A und B unterscheiden sich signifikant hinsichtlich ihrer zentralen Tendenz
- Fällt bei ungeradzahligem N = N1 + N2 ein Messwert genau auf den gemeinsamen Median, kann dieser Messwert exkludiert werden
- Ansonsten kann auch ein Paramediantest durchgeführt werden - Dichotomisierung nahe am Median, um zu verhindern, dass Messwerte mit dem Trennwert identisch sind (vgl. Bortz & Lienert, 2008, S. 137)
- In SPSS wird eine Aufteilung in die Gruppen > Median und
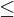 Median vorgenommen
Median vorgenommen
- Mediantest kann auch einseitig durchgeführt werden (beim Vergleich zweier Stichproben, df = 1) - Halbierung des p-Wertes
- Kann auch sehr einfach für den Vergleich von k > 2 Gruppen erweitert werden - keine Vier-Felder-Tafel, sondern k × 2 -Kontingenztafel
- Mediantest findet sich deshalb in SPSS unter Verfahren zum Vergleich von mehr als 2 Stichproben
Tags: Mediantest, nicht-parametrische Verfahren
Source: VO09
Source: VO09
Was zeigt dieser SPSS Ausdruck:


Mediantest prüft 2 unabhängige Stichproben auf Unterschiede in ihrer zentralen Tendenz


Tags: Mediantest, nicht-parametrische Verfahren, SPSS
Source: VO09
Source: VO09
Was prüft der U-Test?
Nicht-parametrische Verfahren / 2 unabhängige Stichproben
U-Test (Mann & Whitney, 1947; auch Wilcoxon-Rangsummentest [Wilcoxon, 1945] genannt) ist das nicht-parametrische Pendant zum t-Test für unabhängige Stichproben
U-Test (Mann & Whitney, 1947; auch Wilcoxon-Rangsummentest [Wilcoxon, 1945] genannt) ist das nicht-parametrische Pendant zum t-Test für unabhängige Stichproben
- Prüft zwei unabhängige Verteilungen auf Unterschiede hinsichtlich ihrer zentralen Tendenz
- H0: Die beiden Stichproben stammen aus formgleich (homomer) verteilten Populationen mit gleichem Median
- U-Test macht Annahme, dass die Form beider Verteilungen gleich ist (Unterschied zum Mediantest! Verteilungen müssen aber nicht symmetrisch oder gar normal sein)
- Verwendet Ranginformation der Daten geeignet für (originär) ordinalskalierte und metrische abhängige Variablen
Tags: nicht-parametrische Verfahren, U-Test
Source: VO09
Source: VO09
Was sind die Prinzipien des U-Test? Wie wird er berechnet?
Prinzip des U-Tests:
Rational: Wenn sich die Stichproben nicht in ihrer zentralen Tendenz (Median) unterscheiden, unterscheiden sie sich auch nicht in ihren mittleren Rängen



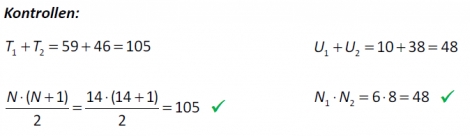
Unser Beispiel: U = 10, exakter Test, zweiseitig: p = .081 /einseitig: p = .041
- Die Messwerte beider Stichproben werden in eine gemeinsame Rangreihe gebracht (kleine Messwerte = niedrige Ränge)
- Rangsumme (U-Test) bzw. mittleren Rangplatz (Wilcoxon- Rangsummentest) pro Gruppe bestimmen
- Bestimmung der statistischen Größe U anhand der Rangsummen bzw. von W anhand der mittleren Ränge- inferenzstatistische Absicherung
Rational: Wenn sich die Stichproben nicht in ihrer zentralen Tendenz (Median) unterscheiden, unterscheiden sie sich auch nicht in ihren mittleren Rängen




- Exakter Test für N1 ≤ N2 ≤ 20 Tabellen in Lehrbüchern bei händischer Berechnung
- Asymptotischer Test für größere Stichproben

Unser Beispiel: U = 10, exakter Test, zweiseitig: p = .081 /einseitig: p = .041
Tags: nicht-parametrische Verfahren, U-Test
Source: VO09
Source: VO09
Was sind Vorteile des U-Tests gegenüber dem Mediantest? Wann sollte jedoch der Mediantest verwendet werden (4 Gründe)?
U-Test hat höhere Testmacht – wenn seine Voraussetzungen zutreffen – als Mediantest (nutzt mehr Information aus den Daten).
U-Test verliert an Macht und Gültigkeit, wenn (vgl. Bortz & Lienert, 2008)
... in diesen Fällen eher Mediantest verwenden
Das Vorliegen von Bindungen beeinträchtigt ebenso die Prüfgröße U - Bindungen sollten für Signifikanztestung berücksichtigt werden
U-Test verliert an Macht und Gültigkeit, wenn (vgl. Bortz & Lienert, 2008)
- Ausreißer vorliegen
- Stichproben ungleich groß sind
- Daten in kleinerer Stichprobe mehr streuen als in größerer
- Boden- oder Deckeneffekte vorliegen
... in diesen Fällen eher Mediantest verwenden
Das Vorliegen von Bindungen beeinträchtigt ebenso die Prüfgröße U - Bindungen sollten für Signifikanztestung berücksichtigt werden
Tags: Mediantest, nicht-parametrische Verfahren, U-Test
Source: VO09
Source: VO09
Wann spricht man von einer Bindung? Und wie muss dies bei einem U-Test berücksichtigt werden?
Das Vorliegen von Bindungen beeinträchtigt die Prüfgröße U - Bindungen sollten für Signifikanztestung berücksichtigt werden
Bindungen treten auf, wenn gleichgroße Messwerte vorliegen - Messwerte „teilen“ sich dann Rangplätze

Alle drei Messwerte haben gleichen Rang (da gleichgroß)
Die Plätze 7, 8 und 9 werden für sie vergeben

Bindungskorrektur verkleinert Varianzschätzung ( ) der Prüfgröße U - Korrektur führt eher zur Verwerfung der H0 (vgl. Bortz & Lienert, 2008, S. 146)
) der Prüfgröße U - Korrektur führt eher zur Verwerfung der H0 (vgl. Bortz & Lienert, 2008, S. 146)
Bindungen treten auf, wenn gleichgroße Messwerte vorliegen - Messwerte „teilen“ sich dann Rangplätze

Alle drei Messwerte haben gleichen Rang (da gleichgroß)
Die Plätze 7, 8 und 9 werden für sie vergeben

Bindungskorrektur verkleinert Varianzschätzung (
 ) der Prüfgröße U - Korrektur führt eher zur Verwerfung der H0 (vgl. Bortz & Lienert, 2008, S. 146)
) der Prüfgröße U - Korrektur führt eher zur Verwerfung der H0 (vgl. Bortz & Lienert, 2008, S. 146)Tags: Bindung, nicht-parametrische Verfahren, U-Test
Source: VO09
Source: VO09
Welche Möglichkeiten (3) gibt es zur Berechnung der Effektgröße für den U-Test?
Für U-Test existiert keine eigenständige Definition einer Effektgröße
Allerdings:
Allerdings:
- Berechnung und Angabe des sog. relativen Effekts mithilfe der mittleren Rangsummen (Mann & Whitney, 1947)
- Maßzahl der stochastischen Tendenz interpretierbar als Wahrscheinlichkeit, dass eine Person aus Gruppe 2 einen höherer Wert als eine Person aus Gruppe 1 hat
- Weitere Möglichkeit über asymptotische Eigenschaften von U: Verteilung von U kann mithilfe von z-Verteilung (Standardnormalverteilung) approximiert werden - approximative Bestimmung der Effektgröße r


Tags: Effektgröße, nicht-parametrische Verfahren, U-Test
Source: VO09
Source: VO09
Was zeigt dieser SPSS-Ausdruck bzw. die berechneten Werte:




Nicht-parametrische Verfahren: U-Test
Tabelle Ränge:
Angabe der mittleren Ränge und Rangsummen
Blick auf mittlere Ränge erlaubt Überprüfung, in welcher Gruppe niedrigere/höhere Werte vorlagen
Statistik für Test
Äquivalente Teststatistiken U und W, z- und p-Werte

Relativer Effekt interpretierbar als:
Die Wahrscheinlichkeit, dass eine Person aus Gruppe B einen höheren Wert als eine Person aus Gruppe A hat, beträgt (gerundet) nur 21%.
Approximatives Effektmaß deutet auf einen großen Effekt (| r | > .40) hin
Tabelle Ränge:
Angabe der mittleren Ränge und Rangsummen
Blick auf mittlere Ränge erlaubt Überprüfung, in welcher Gruppe niedrigere/höhere Werte vorlagen
Statistik für Test
Äquivalente Teststatistiken U und W, z- und p-Werte

Relativer Effekt interpretierbar als:
Die Wahrscheinlichkeit, dass eine Person aus Gruppe B einen höheren Wert als eine Person aus Gruppe A hat, beträgt (gerundet) nur 21%.
Approximatives Effektmaß deutet auf einen großen Effekt (| r | > .40) hin
Tags: nicht-parametrische Verfahren, SPSS, U-Test
Source: VO09
Source: VO09
Was prüft ein Medientest für k > 2 Stichproben?
Mediantest lässt sich auch für k > 2 Stichproben einsetzen
H0: Die k Stichproben stammen aus Populationen mit gleichem Median

H0: Die k Stichproben stammen aus Populationen mit gleichem Median
- Alternativhypothese hier nur ungerichtet möglich (Omnibustest, vgl. einfaktorielle ANOVA)
- Grundlage ist keine Vier-Felder-Tafel, sondern eine k × 2-Tafel

Tags: Mediantest, nicht-parametrische Verfahren
Source: VO09
Source: VO09
Was zeigt dieser SPSS-Ausdruck:




Nicht-parametrische Verfahren / k > 2 unabhängige Stichproben: Mediantest

Testergebnis:
Gemeinsamer Median = 10

Testergebnis:
Gemeinsamer Median = 10
- signifikanter Unterschied im Test über alle drei Gruppen; stärkere Wirkung von Präparaten A und B gegenüber C (aus Kontingenztafel gefolgert)
- ANOVA: p = .122 nicht signifikant
- Exakter Test notwendig, da in allen 6 Zellen die erwarteten Häufigkeiten < 5 sind!
Tags: Mediantest, nicht-parametrische Verfahren
Source: VO09
Source: VO09
Was prüft der Kruska-Wallis-Test? Wie wird dieser noch genannt?
Kruskal-Wallis-Test (H-Test; Kruskal & Wallis, 1952) ist Verallgemeinerung der Prinzipien des U-Test für k > 2 Stichproben
„klassisches“ Pendant der einfaktoriellen ANOVA
H0: Die k Stichproben stammen aus formgleich (homomer) verteilten Populationen mit gleichem Median
H-Test beruht ebenso auf Berechnung von Rangsummen und mittleren Rängen wie U-Test und Wilcoxon-Rangsummentest
Teststatistik H (bei größeren Stichproben) χ2-verteilt, mit df = k − 1

„klassisches“ Pendant der einfaktoriellen ANOVA
H0: Die k Stichproben stammen aus formgleich (homomer) verteilten Populationen mit gleichem Median
H-Test beruht ebenso auf Berechnung von Rangsummen und mittleren Rängen wie U-Test und Wilcoxon-Rangsummentest
Teststatistik H (bei größeren Stichproben) χ2-verteilt, mit df = k − 1

- Ebenso wie für U-Test gibt es eine Bindungskorrektur - vergrößert Wert der Teststatistik, führt eher zur Verwerfung der H0
- Alternativhypothese des H-Tests nur ungerichtet (Omnibustest)
- Bei kleinen Stichproben exakter Test, ansonsten asymptotischer Test - Asymptotischer Test hinreichend genau, wenn kleinste Stichprobe > 5
- Mediantest kann (ebenso wie im Fall k = 2) auch im Fall k > 2 mächtiger sein als H-Test; i. A. hat H-Test aber mehr Macht (mehr Information)
Tags: H-Test, Kruska-Wallis-Test, nicht-parametrische Verfahren
Source: VO10
Source: VO10
Wie lassen sich beim Kruska-Wallis-Test (H-Test) Effekte berechnen?
Analog zu U-Test lassen sich relative Effekte berechnen

Stochastische Tendenz, dass Personen der j-ten Gruppe höhere Werte als durchschnittlich alle anderen Gruppen erzielten
Welche Gruppen sich bei signifikantem Omnibustest signifikant
voneinander unterscheiden, kann im H-Test (analog zur ANOVA) mittels Kontrasten und Post-Hoc-Prozeduren untersucht werden.

Stochastische Tendenz, dass Personen der j-ten Gruppe höhere Werte als durchschnittlich alle anderen Gruppen erzielten
Welche Gruppen sich bei signifikantem Omnibustest signifikant
voneinander unterscheiden, kann im H-Test (analog zur ANOVA) mittels Kontrasten und Post-Hoc-Prozeduren untersucht werden.
Tags: H-Test, Kruska-Wallis-Test, nicht-parametrische Verfahren
Source: VO10
Source: VO10
Wie lässt sich bei einem Kruska-Wallis-Test (H-Test) der familywise error kontrollieren? Beschreibe diese.
Familywise error wird implizit (Kontraste) oder explizit (Post-Hoc-Tests) kontrolliert.
Kontraste
Berechnung der kritischen Differenzen

Durch Verwendung von wird eine implizite Fehlerkontrolle angewandt - familywise error bleibt auf gewähltem α-Niveau
wird eine implizite Fehlerkontrolle angewandt - familywise error bleibt auf gewähltem α-Niveau
Post-Hoc-Tests:
2 äquivalente Methoden:
Explizite Fehlerkontrolle: Bonferroni-Korrektur als einfachste Methode:

Kritische Differenzen nach Siegel und Castellan mit expliziter
Fehlerkontrolle

Größe der kritischen Differenzen (implizite/explizite Fehlerkontrolle) abhängig von der Größe der verglichenen Stichproben (= Nj)
Sind Stichproben nicht gleich groß, müssen für jeden Vergleich unterschiedliche kritische Differenzen bestimmt werden
Kontraste
Berechnung der kritischen Differenzen

Durch Verwendung von
 wird eine implizite Fehlerkontrolle angewandt - familywise error bleibt auf gewähltem α-Niveau
wird eine implizite Fehlerkontrolle angewandt - familywise error bleibt auf gewähltem α-NiveauPost-Hoc-Tests:
2 äquivalente Methoden:
- Testung aller interessierenden (!) Vergleiche mittels U-Tests
- Bestimmung der kritischen Differenzen nach Siegel und Castellan (1988)
Explizite Fehlerkontrolle: Bonferroni-Korrektur als einfachste Methode:

- Werden alle k Gruppen miteinander verglichen, kann α* sehr niedrig und die Testung damit sehr konservativ werden !
- A priori Auswahl und Beschränkung auf jene Vergleiche, die von Interesse sind - m‘ (= Anzahl dieser Vergleiche) ist dann kleiner als m und Testung damit weniger konservativ
Kritische Differenzen nach Siegel und Castellan mit expliziter
Fehlerkontrolle

-
 ist kritischer z-Wert von α* - kann aus Tabellen abgelesen werden
ist kritischer z-Wert von α* - kann aus Tabellen abgelesen werden - Vorgehen ist äquivalent zur Anwendung sequentieller U-Tests
Größe der kritischen Differenzen (implizite/explizite Fehlerkontrolle) abhängig von der Größe der verglichenen Stichproben (= Nj)
Sind Stichproben nicht gleich groß, müssen für jeden Vergleich unterschiedliche kritische Differenzen bestimmt werden
Tags: Effektgröße, H-Test, Kontrast, Kruska-Wallis-Test, Post-Hoc-Test
Source: VO10
Source: VO10
Was zeigt der SPSS-Ausdruck zu diesem Beispiel:
In Untersuchung der BDI-Werte von Depressiven, Remittierten und Gesunden war in der Gruppe der Gesunden keine Normalverteilung gegeben.
Kann Ergebnis der ANOVA mit nicht-parametrischen Methoden bestätigt werden?


In Untersuchung der BDI-Werte von Depressiven, Remittierten und Gesunden war in der Gruppe der Gesunden keine Normalverteilung gegeben.
Kann Ergebnis der ANOVA mit nicht-parametrischen Methoden bestätigt werden?


Ränge:
Mittlere Ränge: niedrigste bei den Gesunden, höchste bei den Depressiven
Statistik für Test
Testergebnis signifikant - p < .001
Zum Vergleich:
Mediantest ebenso signifikant (p < .001), geringere Testmacht zeigt sich aber in niedrigerem χ2-Wert (χ2 = 58.65, df = 2)
Mittlere Ränge: niedrigste bei den Gesunden, höchste bei den Depressiven
Statistik für Test
Testergebnis signifikant - p < .001
Zum Vergleich:
Mediantest ebenso signifikant (p < .001), geringere Testmacht zeigt sich aber in niedrigerem χ2-Wert (χ2 = 58.65, df = 2)
Tags: H-Test, Kruska-Wallis-Test, nicht-parametrische Verfahren, SPSS
Source: VO10
Source: VO10
Wie kann man die relativen Effekte bei diesem Beispiel interpretieren?




Gesunde haben die niedrigste Wahrscheinlichkeit höhere Werte als alle anderen aufzuweisen, Depressive haben die höchste Wahrscheinlichkeit
Tags: Effektgröße, H-Test, Kruska-Wallis-Test, nicht-parametrische Verfahren
Source: VO10
Source: VO10
Was prüft der Jonckheere-Terpstra-Test? Welche Voraussetzung hat dieser?
Ähnlich wie in ANOVA kann auch nicht-parametrisch das Vorhandensein eines (monotonen) Trends untersucht werden - Jonckheere-Terpstra-Test
Test „funktioniert“ ähnlich wie H-Test (ist ebenso ein Omnibustest;
gleiche H0):
Test „funktioniert“ ähnlich wie H-Test (ist ebenso ein Omnibustest;
gleiche H0):
- H0: Die k Stichproben stammen aus formgleich (homomer) verteilten Populationen mit gleichem Median
- Allerdings wird auch eine Rangordnung in der unabhängigen Variable angenommen - Testrational entspricht einem additiven Verfahren einseitiger U-Tests
- H1: Die Mediane der k Stichproben folgen einer schwach monotonen Rangordnung:
 (an zumindest einer Stelle muss das „
(an zumindest einer Stelle muss das „
 “ durch ein „
“ durch ein „ “ ersetzbar sein)
“ ersetzbar sein)- Anwendung des Jonckheere-Terpstra-Test setzt voraus, dass schon a priori Annahmen zur Rangreihung der unabhängigen Variable vorliegen (wie in ANOVA) - Prüfung dieser Annahme, keine a posteriori Bestätigung !
- Verfahren führt (asymptotisch, wenn N groß genug) zu einer z-verteilten Prüfstatistik
- Für Testung in SPSS muss die unabhängige Variable so kodiert sein, dass sie der zu testenden Rangreihung entspricht (analog in ANOVA)
Tags: Jonckheere-Terpstra-Test, nicht-parametrische Verfahren
Source: VO10
Source: VO10
Was zeigt dieser SPSS-Ausdruck:


nicht-parametrische Verfahren / k > 2 unabhängige Stichproben: Jonckheere-Terpstra-Test
- J-T-Statistiken dienen der Berechnung einer z-verteilten Prüfvariable („standardisierte J-TStatistik“)
- „Asymptotische Signifikanz“ basiert auf der Heranziehung der Standardnormalverteilung als Prüfverteilung - p < .001; die Mediane weisen eine monotone Ordnung auf(zur Erinnerung: Depressive = 31.50, Remittierte = 17,Gesunde = 7)
Tags: Jonckheere-Terpstra-Test, nicht-parametrische Verfahren, SPSS
Source: VO10
Source: VO10
Was prüft der McNemar-Test? Wann wird dieser angewendet?
Nicht-parametrische Verfahren / 2 abhängige Stichproben:
McNemar-Test (McNemar, 1947) ist einfachstes nicht-parametrisches Verfahren zur Untersuchung dichotomer Merkmale in 2 abhängigen Stichproben (Test zweier abhängiger prozentualer Anteile)
- Häufigkeitentest, χ2-Test (basiert auf einer 4-Felder-Tafel)
Anwendung des McNemar-Test richtet sich nach dem Vorliegen abhängiger Datenstrukturen:
McNemar-Test (McNemar, 1947) ist einfachstes nicht-parametrisches Verfahren zur Untersuchung dichotomer Merkmale in 2 abhängigen Stichproben (Test zweier abhängiger prozentualer Anteile)
- Häufigkeitentest, χ2-Test (basiert auf einer 4-Felder-Tafel)
Anwendung des McNemar-Test richtet sich nach dem Vorliegen abhängiger Datenstrukturen:
- Ein Merkmal wird mehrfach gemessen (Veränderungsmessung)
- Zwei Stichproben werden parallelisiert (matched samples) -Aussagen dazu, ob ein Merkmal in einer Stichprobe häufiger vorhanden ist, als in der anderen
- Vergleich der Zuwachsraten von zwei Merkmalen in einer Stichprobe: verändern sich zwei Merkmale mit unterschiedlicher Häufigkeit durch z.B. eine Behandlung?
Tags: McNemar-Test, nicht-parametrische Verfahren
Source: VO10
Source: VO10
Was ist das Prinzip des McNemar-Tests? Welche Voraussetzungen müssen erfüllt sein?
Nicht-parametrische Verfahren / 2 abhängige Stichproben
Prinzip (Veränderungshypothese):
Voraussetzungen (vgl. χ2-Tests in Kontingenztafeln)
Falls Voraussetzung des asymptotischen Tests nicht gegeben ist, kann Binomialtest (= exakter Test) verwendet werden (mit Parametern p = .5 und N = b + c)
Wie für 4-Felder-Test kann auch eine Kontinuitätskorrektur verwendet werden konservativere Testung.
Prinzip (Veränderungshypothese):
- Wenn sich nichts geändert hat, sollten sich in den Zellen b und c keine Unterschiede zeigen (Zellen a und d tragen keine Information !)
- Erwartungswerte dieser Zellen:

- Inferenzstatistische Untersuchung über Vergleich dieser Erwartungswerte mit den beobachteten Werten in Zellen b und c


Voraussetzungen (vgl. χ2-Tests in Kontingenztafeln)
- Untersuchungsobjekte müssen eindeutig in das 4-Felder-Schema eingeordnet werden können
- Die erwarteten Häufigkeiten der Felder b und c sind > 5 (asymptotischer Test!)
Falls Voraussetzung des asymptotischen Tests nicht gegeben ist, kann Binomialtest (= exakter Test) verwendet werden (mit Parametern p = .5 und N = b + c)
Wie für 4-Felder-Test kann auch eine Kontinuitätskorrektur verwendet werden konservativere Testung.
Tags: McNemar-Test, nicht-parametrische Verfahren
Source: VO10
Source: VO10
Interpretiere den untenstehenden SPSS-Ausdruck für folgendes Beispiel:
Beispiel: (vgl. Meyer et al., 2005)
Kardiovaskuläre Erkrankungen bei Patienten mit Schizophrenie oder schizoaffektiven Störungen ein wichtiger Morbiditäts- und Mortalitätsfaktor. Metabolisches Syndrom (Fettleibigkeit, Hypertonie, veränderte Blutfettwerte, Insulinresistenz) ist ein Risikofaktor für kardiovaskuläre Erkrankungen. Unterschiedliche antipsychotische Medikamente nehmen unterschiedlichen Einfluss auf das Körpergewicht und das metabolische Syndrom.
Bewirkt die Gabe eines bestimmten Antipsychotikums (Risperidon vs. Olanzapin) eine Verringerung der Auftrittshäufigkeit eines metabolischen Syndroms (= Met S) bei übergewichtigen Risikopatienten (BMI > 26)?

Beispiel: (vgl. Meyer et al., 2005)
Kardiovaskuläre Erkrankungen bei Patienten mit Schizophrenie oder schizoaffektiven Störungen ein wichtiger Morbiditäts- und Mortalitätsfaktor. Metabolisches Syndrom (Fettleibigkeit, Hypertonie, veränderte Blutfettwerte, Insulinresistenz) ist ein Risikofaktor für kardiovaskuläre Erkrankungen. Unterschiedliche antipsychotische Medikamente nehmen unterschiedlichen Einfluss auf das Körpergewicht und das metabolische Syndrom.
Bewirkt die Gabe eines bestimmten Antipsychotikums (Risperidon vs. Olanzapin) eine Verringerung der Auftrittshäufigkeit eines metabolischen Syndroms (= Met S) bei übergewichtigen Risikopatienten (BMI > 26)?

Kreuztabelle:
Kreuztabelle mit den absoluten Häufigkeiten
Tabelle Chi-Quadrat-Test:
Exakter Test (= Binomialtest) wird durchgeführt
p = .008 (2-seitig) p = .004 (1-seitig)
= signifikantes Ergebnis - Es zeigt sich eine eindeutige Verringerung der Auftrittshäufigkeit eines metabolischen Syndroms.
Voraussetzung für McNemar-Test: Die erwarteten Häufigkeiten der Felder b und c sind > 5 (asymptotischer Test!)
Falls Voraussetzung des asymptotischen Tests nicht gegeben ist, kann Binomialtest (= exakter Test) verwendet werden.
Kreuztabelle mit den absoluten Häufigkeiten
Tabelle Chi-Quadrat-Test:
Exakter Test (= Binomialtest) wird durchgeführt
p = .008 (2-seitig) p = .004 (1-seitig)
= signifikantes Ergebnis - Es zeigt sich eine eindeutige Verringerung der Auftrittshäufigkeit eines metabolischen Syndroms.
Voraussetzung für McNemar-Test: Die erwarteten Häufigkeiten der Felder b und c sind > 5 (asymptotischer Test!)
Falls Voraussetzung des asymptotischen Tests nicht gegeben ist, kann Binomialtest (= exakter Test) verwendet werden.
Tags: McNemar-Test, nicht-parametrische Verfahren, SPSS
Source: VO10
Source: VO10
Welche Tests (2) ähnlich dem McNemar-Test können durchgeführt werden? Wann werden diese angewendet?
- Bowker-Test Prinzip des McNemar-Test kann auch auf Merkmale mit mehr als 2 Kategorien erweitert werden.Bowker-Test ein Omnibustest und kann nur ungerichtet durchgeführt werden (df > 1 !)Wird in SPSS automatisch durchgeführt, wenn „McNemar“ angewählt wird und das untersuchte Merkmal mehr als 2 Kategorien aufweist.
- Q-Test von Cochran Ebenso kann Prinzip des McNemar-Test auf mehr als 2 dichotome (abhängige) Merkmale erweitert werdenQ-Test auch ein Omnibustest (nur ungerichtete H1).
Tags: McNemar-Test, nicht-parametrische Verfahrenh
Source: VO10
Source: VO10
Was ist der Vorzeichentest? (Kennzeichen, H0, Prinzip)
- Vorzeichentest einer der ältesten nicht-parametrischen Tests überhaupt
- Geeignet für (originär) ordinalskalierte oder metrische Daten
- H0: Der erste Wert eines Messwertpaares ist mit der gleichen Wahrscheinlichkeit (p = .5) größer oder kleiner als der zweite Messwert(Bezieht sich nicht wie die meisten anderen Tests auf Mediane sondern auf MITTELWERTE)
- Prinzip des Tests: - Bildung der Differenzen der Messwertepaare- Notieren, ob Differenz positiv (+) oder negativ (−) [oder Null (0)]- Durchführen eines Binomialtests anhand jener Zahl (n+ oder n−), die kleiner ist- Parameter des Binomialtests: p = .5, N = n+ + n−
- Vorzeichentest stellt praktisch fast gar keine Voraussetzungen an die Daten - Messgrößen als solche können prinzipiell in ihrer exakten Größe völlig unbekannt sein- Solange eindeutig festgestellt werden kann, ob eine Verbesserung (+), Verschlechterung (−) oder ein Gleichbleiben (0) vorliegt, kann der Test angewandt werden
Tags: nicht-parametrische Verfahren, Vorzeichentest
Source: VO11
Source: VO11
Welche Rolle spielen die Nulldifferenzen beim Vorzeichentest?
Problematisch kann es sein, wenn viele Nulldifferenzen vorliegen
- Ausschließen aus der Testung begünstigt tendenziell die Verwerfung der H0
- Alternativ kann die Hälfte der Nulldifferenzen ein positives, die andere Hälfte ein negatives Vorzeichen erhalten und in die Testung inkludiert werden
Tags: nicht-parametrische Verfahren, Nulldifferenzen, Vorzeichentest
Source: VO11
Source: VO11
Was zeigt dieser SPSS-Ausdruck:


(Nicht parametrische Verfahren / 2 abhängige Stichproben: Vorzeichentest )
Tabelle Häufigkeiten:
Tabelle Statistik für Tests:
Asymptotischer Test (N groß genug) wird durchgeführt
p < .001 (2-seitig) p < .001 (1-seitig)
Tabelle Häufigkeiten:
- 53 Patienten zeigten eine Verbesserung (T2 < T1 „Negative Differenzen“)
- 3 Patienten zeigten eine Verschlechterung (T2 > T1 „Positive Differenzen“)
- 0 Patienten blieben gleich („Bindungen“)
Tabelle Statistik für Tests:
Asymptotischer Test (N groß genug) wird durchgeführt
p < .001 (2-seitig) p < .001 (1-seitig)
Tags: abhängige Daten, nicht-parametrische Verfahren, SPss
Source: VO11
Source: VO11
Was ist der Wilcoxon-Test? Was ist das Prinzip des Tests?
(nicht parametrische Verfahren: 2 abhängige Stichproben)
Wilcoxon-Test (Wilcoxon, 1945; auch Vorzeichenrangtest genannt) das Pendant des t-Tests für abhängige Stichproben
Prinzip des Tests:
Beispiel:

Rangsummen:
T(+) = 49
T(−) = 17

Wilcoxon-Test (Wilcoxon, 1945; auch Vorzeichenrangtest genannt) das Pendant des t-Tests für abhängige Stichproben
- Geeignet nur für metrische Daten
- H0: Die beiden abhängigen Stichproben stammen aus Verteilungen mit gleichem Median
Prinzip des Tests:
- Bildung der Differenzen di der Messwertepaare
- Rangreihung der absoluten Differenzen
- Notieren, ob Differenz positiv (+) oder negativ (−) [oder Null (0)]
- Bestimmung der positiven und negativen Rangsummen (vgl. U-Test) - Inferenzstatistische Absicherung
Beispiel:

Rangsummen:
T(+) = 49
T(−) = 17

Tags: nicht-parametrische Verfahren, Wilcoxon-Test
Source: VO11
Source: VO11
Wann wird für den Wilcoxon-Test ein exakter Test bzw. wann ein asymptotischer Test durchgeführt?
Exakter Test für N ≤ 50 Tabellen in Lehrbüchern
Asymptotischer Test für größere Stichproben

Unser Beispiel:
T = 17, exakter Test,
zweiseitig: p = .175
einseitig: p = .087
Asymptotischer Test für größere Stichproben

Unser Beispiel:
T = 17, exakter Test,
zweiseitig: p = .175
einseitig: p = .087
Tags: nicht-parametrische Verfahren, Wilcoxon-Test
Source: VO11
Source: VO11
Welche Rolle spielen Bindungskorrektur und Nulldiffernzen im Wilcoxon-Test?
Was ist der Unterschied zum Vorzeichentest?
Was ist der Unterschied zum Vorzeichentest?
Wie für U-Test gibt es eine Bindungskorrektur (vgl. Bortz & Lienert, 2008, S. 196), wenn gleiche Differenzwerte vorliegen Anwendung der Korrektur führt eher zur Verwerfung der H0
Fälle mit Nulldifferenzen können ebenso wie beim Vorzeichentest
Fälle mit Nulldifferenzen können ebenso wie beim Vorzeichentest
- ausgeschlossen werden (begünstigt tendenziell Verwerfung der H0)
- oder erhalten generell den Rang (p + 1)/2 (p = Anzahl der Nulldifferenzen; vgl. Bortz & Lienert, 2008, S. 196)
- Wilcoxon-Test i. A. effizienter als Vorzeichentest (verwendet mehr Information aus den Daten)
- i. A. robust gegenüber Dispersionsunterschieden in den abhängigen Messungen (Unterschiede in Streuungen haben keine großen Auswirkungen.)
- Allerdings: ─ Hohes Messniveau Voraussetzung des Tests─ Differenzen der Messungen müssen auf einer Intervallskala liegen - metrisches Messniveau erforderlich─ Unterschiede in der Dispersion können u. U. auch Testmachtschmälern - Vorzeichentest kann dann effizienter sein !
- Asymptotische Eigenschaften des Tests können zur Bestimmung einer approximativen Effektgröße wie im U-Test verwendet werden Verwendung des z-Wertes unter Heranziehung der Formel beim U-Test
Tags: nicht-parametrische Verfahren, Wilcoxon-Test
Source: VO11
Source: VO11
Was misst der Friedman-Test?
(Nicht-parametrische Verfahren / k > 2 abhängige Stichproben)
Friedman-Test (Friedman, 1937; auch Rangvarianzanalyse genannt) das nichtparametrische Pendant zur einfaktoriellen abhängigen ANOVA
Beispiel:

Wenn sich die abhängigen Messungen nicht in ihren Rangsummen unterscheiden, unterscheiden sie sich auch nicht in ihrer zentralen Tendenz (Median).
Friedman-Test (Friedman, 1937; auch Rangvarianzanalyse genannt) das nichtparametrische Pendant zur einfaktoriellen abhängigen ANOVA
- H0: Die k abhängigen Stichproben stammen aus Verteilungen mit gleichem Median
- Geeignet für (originär) ordinalskalierte und metrische Daten
- Prinzip des Tests: - Rangreihung der Messungen innerhalb jeder Beobachtungseinheit- Bestimmung der Rangsummen (vgl. U-Test) je Messung - Inferenzstatistische Absicherung
Beispiel:

Wenn sich die abhängigen Messungen nicht in ihren Rangsummen unterscheiden, unterscheiden sie sich auch nicht in ihrer zentralen Tendenz (Median).
- Teststatistik asymptotisch χ2-verteilt, mit df = k − 1 (vgl. Kruskal-Wallis-Test)
- Beispiel führt zu χ2 = 2.57, df = 2, p = .276 (asympt.), p = .305 (exakt) (2,57 – ist nicht signifikant – vielleicht ist die Stichprobe zu klein bzw. die Unterschiede zu klein.)
- Bindungskorrektur möglich (vgl. Bortz & Lienert, 2008, S. 205) - führt eher zur Verwerfung der H0
- Alternativhypothese des Friedman-Tests nur ungerichtet (Omnibustest)
- Bei kleinen Stichproben exakter Test

Tags: Friedman-Test, nicht-parametrische Verfahren
Source: VO11
Source: VO11
Wie können Kontraste und Post-Hoc-Tests für den Friedman-Test angewendet werden?
Kontraste
Post-Hoc-Tests
Beispiel: (vgl. Wilkinson-Tough et al., 2009)
Fallserie zur Untersuchung der Wirkung einer Mindfulness-basierten Therapiemethode bei Patienten mit Zwangsgedanken 7 Patienten, die im Rahmen eines A-B-C-Designs zunächst eine Phase ohne Behandlung (Phase A; 2 Wochen; Baseline), dann eine Phase in der sie angeleitet und selbständig Progressive Muskelrelaxation anwandten (Phase B; 2-3 Wochen; PMR) und eine Phase in der sie schließlich 6 wöchentliche einstündige Therapieeinheiten mit Psychoedukation und Mindfulness-basierter Psychotherapie erhielten (Phase C; 6 Wochen; Mindfulness). Die Patienten wurden aufgefordert, die in den Therapiephasen gelernten Übungen selbständig weiterzuführen. Zwei Monate nach Ende von Phase C wurde eine Katamnese durchgeführt.
Primäres Outcomemaß: YBOCS (Yale-Brown Obsessive-Compulsive Scale; Werte > 15 klinisch relevant)


- Wie im Fall des Kruskal-Wallis-Test Berechnung kritischer Differenzen der mittleren Rangsummen
- Durch Verwendung des kritischen Wertes wird eine implizite Fehlerkontrolle angewandt familywise error bleibt auf gewähltemα-Niveau

Post-Hoc-Tests
- Kritische Differenzen mit expliziter Fehlerkontrolle
- zα* ist kritischer z-Wert von α* (= Bonferroni-korrigiertes α) kann aus Tabellen abgelesen werden
- Vorgehen ist laut Field (2009) (im Wesentlichen) äquivalent zur Anwendung sequentieller Wilcoxon-Tests - stimmt nur bedingt, Voraussetzungen des Friedman- und des Wilcoxon-Tests sind nicht ident !

Beispiel: (vgl. Wilkinson-Tough et al., 2009)
Fallserie zur Untersuchung der Wirkung einer Mindfulness-basierten Therapiemethode bei Patienten mit Zwangsgedanken 7 Patienten, die im Rahmen eines A-B-C-Designs zunächst eine Phase ohne Behandlung (Phase A; 2 Wochen; Baseline), dann eine Phase in der sie angeleitet und selbständig Progressive Muskelrelaxation anwandten (Phase B; 2-3 Wochen; PMR) und eine Phase in der sie schließlich 6 wöchentliche einstündige Therapieeinheiten mit Psychoedukation und Mindfulness-basierter Psychotherapie erhielten (Phase C; 6 Wochen; Mindfulness). Die Patienten wurden aufgefordert, die in den Therapiephasen gelernten Übungen selbständig weiterzuführen. Zwei Monate nach Ende von Phase C wurde eine Katamnese durchgeführt.
Primäres Outcomemaß: YBOCS (Yale-Brown Obsessive-Compulsive Scale; Werte > 15 klinisch relevant)

- Kontraste: eine kritische Differenz für alle Einzelvergleiche kritischer χ2-Wert (α = .05, df = 3): 7.81
- Post-Hoc-Tests: Wilcoxon-Tests, α* = .05/3 = .017
- Effektstärken: anhand der z-Werte der Wilcoxon-Tests (sehr approximativ!!!)

Tags: Friedman-Test, Kontrast, nicht-parametrische Verfahren, Post-Hoc-Test
Source: VO11
Source: VO11
Was zeigt dieser SPSS-Ausdruck:


Ausgabe mittlerer Ränge (oben)
Nach der Mindfulness-Intervention sind die Werte am niedrigsten;
die höchstenWerte liegen zu Beginn vor (Baseline)
Tabelle Statistik für Test
Die H0 wird verworfen, p < .001 (asymptotischer Test)
Nach der Mindfulness-Intervention sind die Werte am niedrigsten;
die höchstenWerte liegen zu Beginn vor (Baseline)
Tabelle Statistik für Test
Die H0 wird verworfen, p < .001 (asymptotischer Test)
Tags: Friedman-Test, nicht-parametrische Verfahren, SPSS
Source: VO11
Source: VO11
Flashcard set info:
Author: coster
Main topic: Psychologie
Topic: Statistik
School / Univ.: Universität Wien
City: Wien
Published: 21.06.2013
Card tags:
All cards (175)
4-Felder-Tafel (17)
abhängige Daten (6)
ALM (1)
ANCOVA (3)
ANOVA (15)
Bindung (1)
Cohens d (10)
Cohens Kappa (6)
Effektgröße (31)
Einzelvergleich (2)
Einzelvergleiche (1)
Eta (7)
Fehler (1)
Friedman-Test (3)
H-Test (5)
Haupteffekt (2)
Haupteffekte (1)
Interaktion (5)
Konkordanz (4)
Kontrast (11)
Kontrollvariable (1)
MANOVA (2)
McNemar-Test (4)
Mediantest (5)
Medientest (1)
mixed ANOVA (10)
NNT (3)
Normalverteilung (3)
NPV (4)
Nulldifferenzen (1)
odds ratio (7)
partielle Eta (5)
phi-Koeffizient (1)
Phi-Koeffizienz (1)
Planung (1)
Post-Hoc-Test (4)
Post-hoc-Tests (3)
Power (1)
PPV (4)
Prävalenz (6)
r (4)
Reliabilität (1)
risk ratio (7)
Sensitivität (6)
Signifikanz (6)
Spezifität (6)
Sphärizität (2)
SPSS (14)
SPss (1)
Stichprobe (3)
Störvariable (1)
t-Test (7)
Testmacht (2)
Trends (1)
U-Test (6)
Varianz (2)
Varianzanalyse (11)
Varianzschätzer (1)
Voraussetzungen (2)
Vorzeichentest (2)
Wechselwirkung (3)
Wilcoxon-Test (4)
x2-Test (5)











